ΟΡΙΣΜΟΙ - ΘΕΩΡΗΜΑ ΥΠΑΡΞΗΣ ΚΑΙ
ΜΟΝΑΔΙΚΟΤΗΤΑΣ ΤΗΣ ΛΥΣΗΣ
Ορισμός 1.
Μια
διαφορική εξίσωση της μορφής
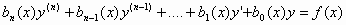 , (1)
, (1)
όπου οι
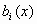
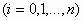 και
και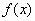 είναι δοθείσες πραγματικές
συναρτήσεις ορισμένες σ’ένα ανοικτό
διάστημα
είναι δοθείσες πραγματικές
συναρτήσεις ορισμένες σ’ένα ανοικτό
διάστημα 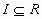 , ονομάζεται
γραμμική διαφορική εξίσωση τάξης n.
, ονομάζεται
γραμμική διαφορική εξίσωση τάξης n.
Ορισμός 2.
Αν 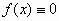 στο διάστημα
στο διάστημα 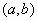 τότε η (1) θα λέγεται ομογενής
ενώ στην αντίθετη περίπτωση
μη-ομογενής. Γενικά,
η συνάρτηση
τότε η (1) θα λέγεται ομογενής
ενώ στην αντίθετη περίπτωση
μη-ομογενής. Γενικά,
η συνάρτηση 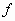 ονομάζεται
μη- ομογενής όρος ή όρος
εξαναγκασμού.
ονομάζεται
μη- ομογενής όρος ή όρος
εξαναγκασμού.
Ορισμός 3.
Ένα σημείο
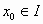 θα
λέγεται ομαλό ή συνηθισμένο
σημείο της (1) αν
θα
λέγεται ομαλό ή συνηθισμένο
σημείο της (1) αν 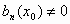 ενώ αν
ενώ αν 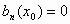 θα λέγεται ανώμαλο ή
ιδιάζον σημείο.
θα λέγεται ανώμαλο ή
ιδιάζον σημείο.
Στη συνέχεια υποθέτουμε ότι όλα τα σημεία
του διαστήματος
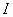 είναι ομαλά σημεία της (1).
Διαιρώντας έτσι με το συντελεστή
είναι ομαλά σημεία της (1).
Διαιρώντας έτσι με το συντελεστή 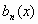 ,
η (1) γράφεται στη μορφή
,
η (1) γράφεται στη μορφή
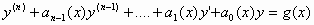 , (2)
, (2)
όπου
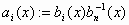
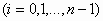 και
και 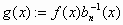 .
.
Για τις διαφορικές εξισώσεις της μορφής (2)
ισχύει το ακόλουθο θεμελιώδες θεώρημα:
Θεώρημα 1.
(Ύπαρξη
και μοναδικότητα της λύσης του προβλήματος
αρχικών τιμών)
Έστω σημείο
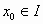 και
τυχαίοι πραγματικοί αριθμοί
και
τυχαίοι πραγματικοί αριθμοί 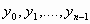 .
Αν οι συναρτήσεις
.
Αν οι συναρτήσεις 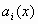
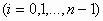 και
και 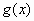 είναι συνεχείς στο
είναι συνεχείς στο 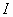 ,
τότε υπάρχει ακριβώς μια
λύση της εξίσωσης (2) η οποία ικανοποιεί τις
αρχικές συνθήκες
,
τότε υπάρχει ακριβώς μια
λύση της εξίσωσης (2) η οποία ικανοποιεί τις
αρχικές συνθήκες
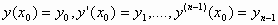 . (3)
. (3)
Ορισμός 4. (Έννοια
της μιγαδικής λύσης)
Έστω
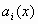
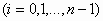 και
και 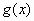 πραγματικές συναρτήσεις
ορισμένες σ’ ένα διάστημα
πραγματικές συναρτήσεις
ορισμένες σ’ ένα διάστημα 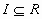 .
Μια μιγαδική συνάρτηση
.
Μια μιγαδική συνάρτηση 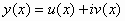 (όπου
(όπου 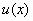 ,
,
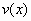 είναι
πραγματικές συναρτήσεις και
είναι
πραγματικές συναρτήσεις και 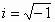 )
θα λέγεται ότι είναι λύση
της εξίσωσης (2) αν και μόνον αν η
)
θα λέγεται ότι είναι λύση
της εξίσωσης (2) αν και μόνον αν η 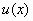 είναι
λύση της (2) και η
είναι
λύση της (2) και η 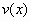 είναι
λύση της αντίστοιχης ομογενούς.
είναι
λύση της αντίστοιχης ομογενούς.
[Επιστροφή
στα Περιεχόμενα]
ΑΣΚΗΣΕΙΣ
:
1. Προσδιορίστε όλες τις λύσεις
του προβλήματος αρχικών τιμών
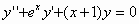 ,
, 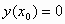 ,
,
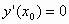 ,
, 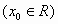 .
.
[Υπόδειξη]
, [Λύση]
2. Το πρόβλημα
αρχικών τιμών
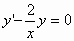 ,
, 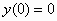 ,
,
έχει ως λύσεις
τις συναρτήσεις 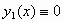 και
και 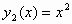 .
Γιατί αυτό δεν έρχεται σε
αντίθεση με το Θεώρημα 1 ;
.
Γιατί αυτό δεν έρχεται σε
αντίθεση με το Θεώρημα 1 ;
[Λύση]
3. Δείξτε ότι το πρόβλημα
αρχικών τιμών
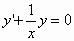 ,
, 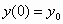 ,
,
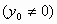 ,
,
δεν έχει λύση.
[Υπόδειξη]
, [Λύση]
[
Επιστροφή
στα Περιεχόμενα]
![]() , (1)
, (1)![]() , (2)
, (2)![]() . (3)
. (3)![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.![]() ,
, ![]() ,
,![]() και
και ![]() .
Γιατί αυτό δεν έρχεται σε
αντίθεση με το Θεώρημα 1 ;
.
Γιατί αυτό δεν έρχεται σε
αντίθεση με το Θεώρημα 1 ; ![]() ,
, ![]() ,
,
![]() ,
,