Η εκθετική συνάρτηση

Υπάρχουν διάφοροι τρόποι ορισμού της εκθετικής και της λογαριθμικής συνάρτησης, έναν από τους οποίους αναφέρουμε εδώ.

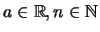
Ορισμός 72   'Εστω $a\in \mathbb R, n\in \mathbb N$. Ορίζουμε

$$a^0 = 1, \; a\not=0, \;\; a^1 = a, \;\; a^{n+1} = a^n.$$

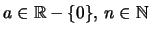
Ορισμός 73   'Εστω $a\in \mathbb R - \{0\}, \, n\in \mathbb N$. Ορίζουμε

$$a^{-n} = \frac{1}{a^n}.$$

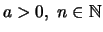
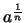
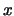
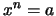
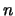
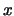
Ορισμός 74   'Εστω $a > 0, \; n\in \mathbb N$. Ορίζουμε $a^{\frac{1}{n}}$ τον μοναδικό θετικό αριθμό $x$ τέτοιον ώστε $x^n = a$. Ο αριθμός αυτός υπάρχει, είναι μοναδικός και λέγεται $n$-οστή ρίζα του $x$ (βλέπε και άσκηση 1).

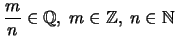
Ορισμός 75   'Εστω $$\frac{m}{n} \in \mathbb Q,\; m \in \mathbb Z, \; n\in \mathbb N$$. Ορίζουμε

$$a^{\frac{m}{n}} = (a^{\frac{1}{n}})^m.$$

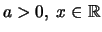
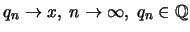
Ορισμός 76   'Εστω $a > 0,\;x\in\mathbb R$ και $q_n \to x,\;n \to \infty,\;q_n\in\mathbb Q$. Ορίζουμε

$$a^{x} = \lim\limits_{n\to \infty}a^{q_n}.$$

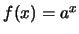
Η συνάρτηση $f(x) = a^x$ ονομάζεται εκθετική συνάρτηση με βάση το $a$.

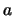
Αποδεικνύεται ότι το παραπάνω όριο υπάρχει και είναι ανεξάρτητο από την ακολουθία 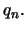$q_n.$

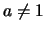
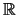
Πρόταση 77   Η εκθετική συνάρτηση είναι γνήσια μονότονη για $a \not = 1$ και παραγωγίσιμη στο $\mathbb R$. Επίσης

$$(e^x)' = e^x$$

και

$$(a^x)' = a^x \log a.$$