Next: 'Ασκηση 4
Up: 'Ασκηση 3
Previous: Υπόδειξη
Λύση
Βρίσκουμε μερικές παραγώγους με σκοπό να  μαντέψουμε
μαντέψουμε τον γενικό τύπο.
'Εχουμε
τον γενικό τύπο.
'Εχουμε
Με επαγωγή θα δείξουμε ότι
Για 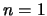 ισχύει.
'Εστω ότι ισχύει για
ισχύει.
'Εστω ότι ισχύει για 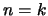 ,
δηλαδή
,
δηλαδή
Θα
δείξουμε ότι ισχύει για 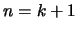 .
Είναι
.
Είναι
και άρα έχουμε την απαιτούμενη σχέση.
'Ασκηση 3
Υπόδειξη
Antonis Tsolomitis
1999-11-11