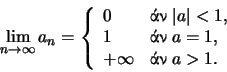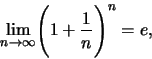Next: Ασκήσεις
Up: Ακολουθίες πραγματικών αριθμών
Previous: Ακολουθίες πραγματικών αριθμών
Ορισμός 7
Ονομάζουμε ακολουθία πραγματικών αριθμών μια συνάρτηση
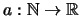
.
Γράφουμε
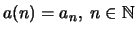
.
Ορισμός 8
Λέμε ότι η ακολουθία
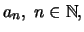
συγκλίνει στο
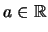
,
αν για
κάθε
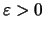
υπάρχει
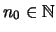
ώστε να έχουμε
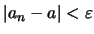
για κάθε
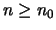
.
Γράφουμε
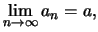
ή
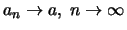
.
Αν μια ακολουθία δεν συγκλίνει σε πραγματικό αριθμό λέμε
ότι αποκλίνει.
Ορισμός 9
Λέμε ότι η ακολουθία
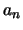
συγκλίνει στο
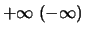
,
αν για κάθε
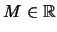
υπάρχει
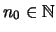
τέτοιο ώστε να έχουμε
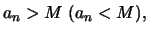
για κάθε
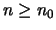
.
Γράφουμε
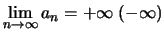
ή
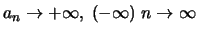
.
Ορισμός 10
Λέμε ότι η ακολουθία
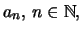
είναι άνω φραγμένη, κάτω φραγμένη,
φραγμένη, αν το σύνολο
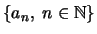
είναι άνω φραγμένο, κάτω φραγμένο,
φραγμένο, αντίστοιχα.
Παρατήρηση. Η χρησιμότητα πολλών από τις προηγούμενες ιδιότητες
βρίσκεται στην εύρεση ορίων χωρίς τον ορισμό, ανάγοντάς τα σε στοιχειώδη.
Ορισμός 12
'Εστω δύο ακολουθίες
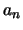
και
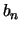
.
Λέμε ότι η
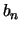
είναι
υπακολουθία της
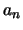
αν υπάρχει μια γνήσια αύξουσα ακολουθία φυσικών αριθμών
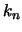
τέτοια ώστε
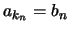
.
Ορισμός 13
Αν μια ακολουθία
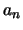
συγκλίνει (ή συγκλίνει στο
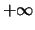
ή στο
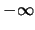
)
τότε κάθε υπακολουθία της συγκλίνει στο ίδιο όριο.
Ορισμός 14
Μια ακολουθία
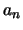
λέγεται αύξουσα (φθίνουσα) αν
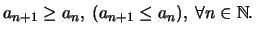
Ορισμός 15
Μια ακολουθία
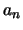
λέγεται γνήσια αύξουσα (γνήσια φθίνουσα) αν
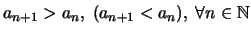
.
Ορισμός 16
Μια ακολουθία
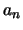
λέγεται μονότονη (γνήσια μονότονη) αν είναι αύξουσα ή φθίνουσα
(γνήσια αύξουσα ή γνήσια φθίνουσα).
Θεώρημα 17
Κάθε μονότονη και φραγμένη ακολουθία συγκλίνει.
Θεώρημα 18
Κάθε μονότονη και μη φραγμένη ακολουθία συγκλίνει
στο
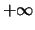
ή στο
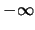
ανάλογα αν είναι αύξουσα ή φθίνουσα.
Θεώρημα 19 (Bolzano - Weierstrass)
Κάθε φραγμένη ακολουθία έχει συγκλίνουσα υπακολουθία.
Ορισμός 20
Μια ακολουθία
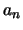
λέγεται ακολουθία Caychy αν για κάθε
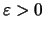
υπάρχει
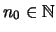
τέτοιος ώστε, να έχουμε
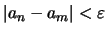
για κάθε
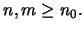
Θεώρημα 21
Μια ακολουθία
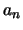
συγκλίνει αν και μόνον αν είναι
ακολουθία Cauchy.
Πρόταση 22
'Εστω η ακολουθία
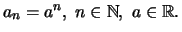
Τότε
Αν
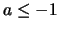
τότε η ακολουθία αποκλίνει.
Πρόταση 24
'Εστω η ακολουθία
![$a_n = \sqrt [n] a, \; a > 0.$](img195.gif)
Τότε
Πρόταση 25
'Εστω η ακολουθία
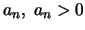
με
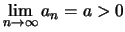
.
Για
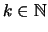
έχουμε
Πρόταση 26
όπου
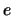
είναι ο αριθμός του Euler,
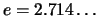
.



Next: Ασκήσεις
Up: Ακολουθίες πραγματικών αριθμών
Previous: Ακολουθίες πραγματικών αριθμών
Antonis Tsolomitis
1999-11-11
![]() και
και
![]() τότε
τότε
![]() (μοναδικότητα του
ορίου).
(μοναδικότητα του
ορίου).
![]() και
και
![]() τότε
τότε
![]() .
.
![]() και
και
![]() τότε
τότε
![]() .
.
![]() και
και
![]() τότε
τότε
![]() .
.
![]() και
και
![]() τότε υπάρχει
τότε υπάρχει
![]() ,
τέτοιο ώστε, για κάθε
,
τέτοιο ώστε, για κάθε ![]() να έχουμε
να έχουμε ![]() και
και
![]()
![]() και
και
![]() τότε
τότε
![]()
![]() και η
και η ![]() είναι φραγμένη
τότε
είναι φραγμένη
τότε
![]() .
.
![]() και
και
![]() τότε
τότε
![]()