


Next: About this document ...
Up: Άσκηση 9
Previous: Υπόδειξη
Λύση
(α)
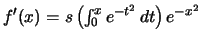 και
και
άρα αν κάνω αλλαγή μεταβλητής θετοντας 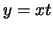 η
η
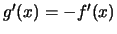 άρα
άρα
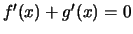 .
.
Επίσης
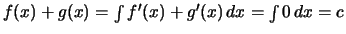 .
Για να βρούμε τη
σταθερά θέτουμε
.
Για να βρούμε τη
σταθερά θέτουμε 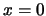 και παίρνουμε
και παίρνουμε 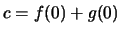 .
Όμως
.
Όμως 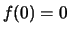 και
και
(β) Άρα
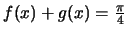 .
Στην τελευταία σχέση του προηγούμενου αφήνουμε το
.
Στην τελευταία σχέση του προηγούμενου αφήνουμε το 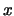 να πάει στο άπειρο.
Όμως,
να πάει στο άπειρο.
Όμως,
Άρα
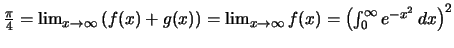 .
.
Έπεται οτι
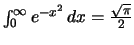 .
.
Άσκηση 9
Υπόδειξη
root
1999-07-29
![]() .
Για να βρούμε τη
σταθερά θέτουμε
.
Για να βρούμε τη
σταθερά θέτουμε ![]() και παίρνουμε
και παίρνουμε ![]() .
Όμως
.
Όμως ![]() και
και
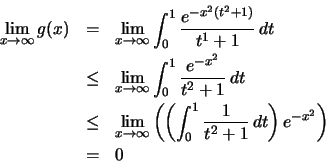
![]() .
.