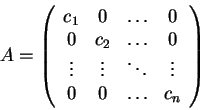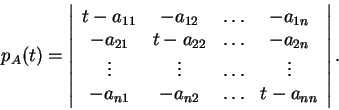Next: Άσκηση 1
Up: Iδιοτιμές - Ιδιοδιανύσματα
Previous: Iδιοτιμές - Ιδιοδιανύσματα
Ορισμός 1
Έστω

διανυσματικός χώρος και
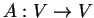
μια γραμμική απεικόνιση. Ένα
στοιχείο
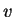
του

λέγεται ιδιοδιάνυσμα του

αν υπάρχει αριθμός
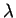
τέτοιος
ώστε
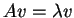
.
Aν το
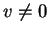
τότε το
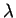
είναι μοναδικά προσδιορισμένο
και λέγεται ιδιοτιμή του
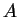
που αντιστοιχεί στο ιδιοδιάνυσμα
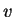
.
Λέμε πολλές
φορές ότι το
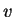
είναι το ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
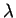
.
Παράδειγμα Aν
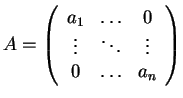 είναι ένας διαγώνιος πίνακας τότε κάθε διάνυσμα
είναι ένας διαγώνιος πίνακας τότε κάθε διάνυσμα
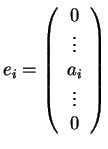 ,
,
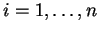 είναι ένα
ιδιοδιάνυσμα του
είναι ένα
ιδιοδιάνυσμα του 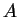 .
Έχουμε
.
Έχουμε 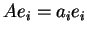 .
.
Θεώρημα 1
Έστω

διανυσματικός χώρος και
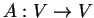
γραμμική απεικόνιση.
Έστω
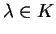
και
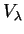
ο υπόχωρος του

που παράγεται από τα ιδιοδιανύσματα του

που αντιστοιχούν στην ιδιοτιμή
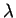
.
Tότε κάθε μη-μηδενικό στοιχείο του
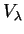
είναι ένα ιδιοδιάνυσμα του

με ιδιοτιμή
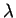
.
Ο υπόχωρος
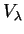
λέγεται ο ιδιόχωρος που αντιστοιχεί στην ιδιοτιμή
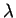
.
Θεώρημα 2
Έστω

ένας διανυσματικός χώρος και
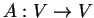
μια γραμμική απεικόνιση.
Έστω
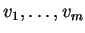
ιδιοδιανύσματα της

με ιδιοτιμές
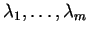
αντίστοιχα. Αν οι ιδιοτιμές είναι διαφορετικές μεταξύ τους, δηλαδή
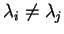
όταν
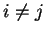
τότε τα
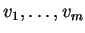
είναι γραμμικά
ανεξάρτητα διανύσματα του

.
Ορισμός 2
Έστω
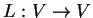
μια γραμμική απεικόνιση.
Αν
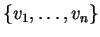
είναι μια βάση του διανυσματικού χώρου

λέμε ότι
η βάση αυτή διαγωνοποιεί την
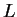
αν κάθε
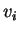
είναι ένα ιδιοδιάνυσμα
της
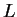
.
Σε αυτή την περίπτωση, ο πίνακας της
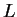
ως προς αυτή την βάση είναι
όπου
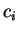
είναι οι ιδιοτιμές που αντιστοιχούν στα ιδιοδιανύσματα
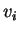
.
Λέμε
ότι η γραμμική απεικόνιση
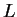
διαγωνοποιήται αν υπάρχει βάση του χώρου

που να αποτελείται από ιδιοδιανύσματα.
Θεώρημα 3
Έστω

ένας διανυσματικός χώρος πεπερασμένης διάστασης και
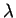
ένας
αριθμός. Αν
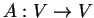
μια γραμμική απεικόνιση τότε ο
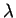
είναι ιδιοτιμή
της

αν και μόνο αν ο πίνακας
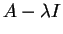
δεν είναι αντιστρέψιμος.
Ορισμός 3
Aν

είναι ένας
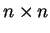
πίνακας, ορίζουμε το χαρακτηριστικό πολυώνυμο
του
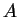
,
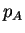
να είναι η ορίζουσα
Θεώρημα 4
Έστω

ένας
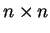
πίνακας. Ένας αριθμός
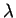
είναι μια
ιδιοτιμή του

αν και μόνο αν το
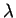
είναι ρίζα του χαρακτηριστικού
πολυωνύμου.
Θεώρημα 5
Aν
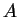
είναι ένας
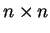
πίνακας με μιγαδικά στοιχεία. Τότε ο

έχει
ένα τουλάχιστον μη μηδενικό ιδιοδιάνυσμα και τουλάχιστον μια μιγαδική
ιδιοτιμή.
Θεώρημα 6
Aν

και
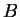
είναι δύο
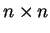
πίνακες και ο
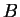
είναι αντιστρέψιμος
τότε το χαρακτηριστικό πολυώνυμο του

είναι ίσο με το χαρακτηριστικό
πολυώνυμο του
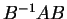
.
Mε άλλα λόγια, όμοιοι πίνακες έχουν το ίδιο
χαρακτηριστικό πολυώνυμο.
Θεώρημα 7 (Cayley - Hamilton)
Mιά γραμμική απεικόνιση
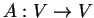
μηδενίζει το χαρακτηριστικό της
πολυώνυμο.
Ορισμός 4
Έστω ένα πολυώνυμο
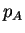
που μηδενίζεται από την απεικόνιση
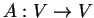
και
έχει πρώτο συντελεστή την μονάδα. Αν κάθε άλλο πολυώνυμο που μηδενίζεται
από την

έχει βαθμό μεγαλύτερο ή ίσο του
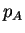
τότε το
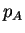
λέγεται ελάχιστο πολυώνυμο της

.
Θεώρημα 8
Tο ελάχιστο πολυώνυμο μιας γραμμικής απεικόνισης είναι μονοσήμαντα
ορισμένο και διαιρεί το χαρακτηριστικό πολυώνυμο της απεικόνισης.
Πρόταση 1
Tο χαρακτηριστικό και το ελάχιστο πολυώνυμο μιας γραμμικής απεικόνισης
έχουν τις ίδιες ρίζες.
Vassilis Metaftsis
1999-09-15
 είναι ένας διαγώνιος πίνακας τότε κάθε διάνυσμα
είναι ένας διαγώνιος πίνακας τότε κάθε διάνυσμα
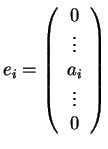 ,
,
![]() είναι ένα
ιδιοδιάνυσμα του
είναι ένα
ιδιοδιάνυσμα του ![]() .
Έχουμε
.
Έχουμε ![]() .
.