


Next: Άσκηση 10
Up: Άσκηση 9
Previous: Υπόδειξη
Έστω 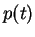 το ελάχιστο πολυώνυμο του
το ελάχιστο πολυώνυμο του 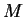 .
Τότε
.
Τότε
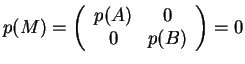 και άρα
και άρα 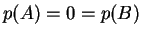 .
Αν
.
Αν 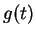 είναι
το ελάχιστο πολυώνυμο του
είναι
το ελάχιστο πολυώνυμο του 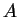 τότε το
τότε το 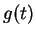 διαιρεί το
διαιρεί το 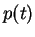 .
Όμοια, αν
.
Όμοια, αν 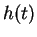 είναι το ελάχιστο πολυώνυμο του
είναι το ελάχιστο πολυώνυμο του 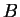 τότε το
τότε το
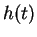 διαιρεί το
διαιρεί το 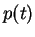 .
Άρα το
.
Άρα το 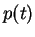 είναι πολλαπλάσιο των
είναι πολλαπλάσιο των
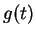 και
και 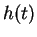 .
.
Έστω τώρα 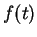 ένα άλλο πολλαπλάσιο των
ένα άλλο πολλαπλάσιο των 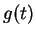 και
και 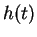 .
Τότε
.
Τότε
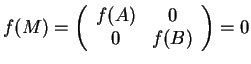 (αφού
(αφού 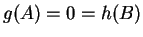 ). Εφόσον το
). Εφόσον το 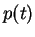 είναι το
ελάχιστο πολυώνυμο έχουμε ότι το
είναι το
ελάχιστο πολυώνυμο έχουμε ότι το 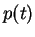 διαιρεί το
διαιρεί το 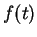 .
Άρα το
.
Άρα το
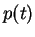 είναι το έλάχιστο κοινό πολλαπλάσιο των
είναι το έλάχιστο κοινό πολλαπλάσιο των 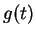 και
και 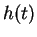 .
.
Vassilis Metaftsis
1999-09-15
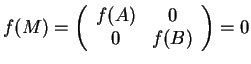 (αφού
(αφού 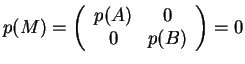 και άρα
και άρα ![]() ένα άλλο πολλαπλάσιο των
ένα άλλο πολλαπλάσιο των ![]() και
και ![]() .
Τότε
.
Τότε
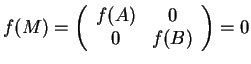 (αφού
(αφού ![]() ). Εφόσον το
). Εφόσον το ![]() είναι το
ελάχιστο πολυώνυμο έχουμε ότι το
είναι το
ελάχιστο πολυώνυμο έχουμε ότι το ![]() διαιρεί το
διαιρεί το ![]() .
Άρα το
.
Άρα το
![]() είναι το έλάχιστο κοινό πολλαπλάσιο των
είναι το έλάχιστο κοινό πολλαπλάσιο των ![]() και
και ![]() .
.