


Next: Άσκηση 22
Up: Άσκηση 21
Previous: Υπόδειξη
Γνωρίζουμε ότι το 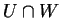 είναι υπόχωρος τόσο του
είναι υπόχωρος τόσο του 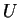 όσο και
του
όσο και
του  .
Υποθέτω ότι dim
.
Υποθέτω ότι dim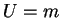 ,
dim
,
dim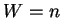 και
dim
και
dim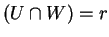 .
Θεωρώ
.
Θεωρώ
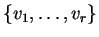 μια βάση του
μια βάση του
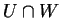 .
Τότε μπορούμε να επεκτείνουμε την παραπάνω βάση σε μια
βάση του
.
Τότε μπορούμε να επεκτείνουμε την παραπάνω βάση σε μια
βάση του 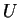 ,
,
και σε
μια βάση του  ,
,
Έστω
To 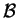 αποτελείται από
αποτελείται από 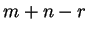 στοιχεία. Θα
δείξουμε ότι το
στοιχεία. Θα
δείξουμε ότι το 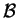 είναι βάση του
είναι βάση του 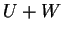 .
Eφόσον το
.
Eφόσον το
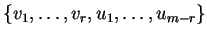 παράγει το
παράγει το 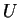 και το
και το
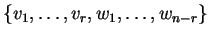 παράγει το
παράγει το  ,
έχουμε
ότι το
,
έχουμε
ότι το 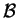 παράγει το
παράγει το 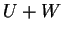 .
Aρκεί να δείξουμε ότι τα
στοιχεία του
.
Aρκεί να δείξουμε ότι τα
στοιχεία του 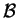 είναι γραμμικώς ανεξάρτητα. Υποθέτω ότι
υπάρχουν
είναι γραμμικώς ανεξάρτητα. Υποθέτω ότι
υπάρχουν 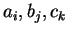 στοιχεία του σώματος
στοιχεία του σώματος  ώστε
ώστε
Έστω
Eφόσον
τα 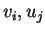 ανήκουν στο
ανήκουν στο 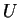 έχουμε ότι το
έχουμε ότι το 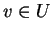 .
Aπό την άλλη,
τα
.
Aπό την άλλη,
τα 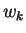 ανήκουν στον
ανήκουν στον  και άρα
και άρα 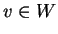 .
Συνεπώς,
.
Συνεπώς, 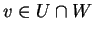 .
Aλλά τα
.
Aλλά τα 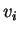 είναι βάση του
είναι βάση του 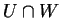 άρα υπάρχουν
πραγματικοί
άρα υπάρχουν
πραγματικοί
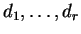 ώστε
ώστε
Aπό
την παραπάνω σχέση για το 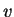 έχουμε ότι
έχουμε ότι
Όμως τα στοιχεία
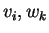 αποτελούν βάση του
αποτελούν βάση του  και άρα είναι γραμμικώς
ανεξάρτητα επομένως
και άρα είναι γραμμικώς
ανεξάρτητα επομένως
Aντικαθιστώντας στην αρχική εξίσωση παίρνουμε
Όμως, τα 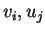 αποτελούν βάση του
αποτελούν βάση του 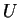 και άρα είναι γραμμικώς ανεξάρτητα επομένως
και άρα είναι γραμμικώς ανεξάρτητα επομένως
Άρα η αρχική εξίσωση
συνεπάγεται ότι τα 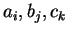 είναι όλα μηδέν και συνεπώς το
είναι όλα μηδέν και συνεπώς το
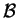 είναι βάση του
είναι βάση του 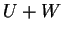 .
.
Vassilis Metaftsis
1999-09-15