


Next: Άσκηση 26
Up: Γραμμικά Συστήματα και Πίνακες
Previous: Γραμμικά Συστήματα και Πίνακες
Ορισμός 14
Έστω

σώμα. Μια διάταξη των στοιχείων του

της μορφής
λέγεται πίνακας με
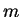
γραμμές και
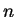
στήλες ή ένας
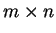
πίνακας.
Αν
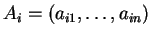
για κάθε
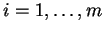
είναι οι γραμμές
του πίνακα και τα
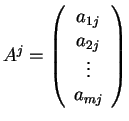
για κάθε
είναι οι στήλες του
πίνακα. O
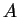
συμβολίζεται και σαν
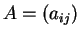
.
Ορισμός 16
Αν

και
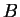
δύο
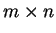
πίνακες, λέμε ότι ο
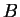
είναι γραμμοϊσοδύναμος
του

αν ο
μπορεί να προκύψει από τον

εφαρμόζοντας μια πεπερασμένη
ακολουθία στοιχειωδών μετασχηματισμών γραμμών.
Παράδειγμα: O πίνακας
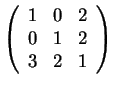 είναι γραμμοϊσοδύναμος με τον πίνακα
είναι γραμμοϊσοδύναμος με τον πίνακα
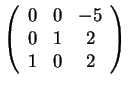 εφόσον
εφόσον
Ορισμός 17
Ένας
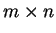
πίνακας

λέγεται κλιμακωτός πίνακας αν
- .
- το πρώτο μη-μηδενικό στοιχείο σε κάθε μη-μηδενική γραμμή είναι 1.
- .
- το πρώτο (ηγετικό) 1 σε κάθε μη-μηδενική γραμμή βρίσκεται στα δεξιά
του ηγετικού 1 κάθε προηγούμενης γραμμής.
- .
- οι μη-μηδενικές γραμμές εμφανίζονται πριν τις μηδενικές γραμμές του
πίνακα.
Ένας κλιμακωτός πίνακας λέγεται αναγμένος αν το ηγετικό 1 σε κάθε μη-μηδενική
γραμμή είναι το μόνο μη-μηδενικό στοιχείο της στήλης στην οποία ανήκει.
Θεώρημα 12
Κάθε μη-μηδενικός πίνακας είναι γραμμοϊσοδύναμος με έναν αναγμένο κλιμακωτό
πίνακα.
Ορισμός 18
Ένα σύστημα της παρακάτω μορφής
με
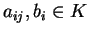
λέγεται σύστημα
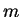
γραμμικών εξισώσεων με
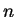
αγνώστους στο σώμα

.
O πίνακας
λέγεται πίνακας του συστήματος και το σύστημα συμβολίζεται
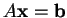
όπου
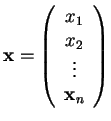
και
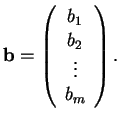
To σύστημα
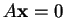
αποκαλείται το ομογενές σύστημα που αντιστοιχεί
στον πίνακα

.
O πίνακας
λέγεται επαυξημένος πίνακας του συστήματος.
Θεώρημα 13
Έστω ένα γραμμικό σύστημα
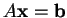
και
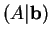
ο επαυξημένος πίνακας
του συστήματος. Αν
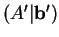
ο πίνακας που προκύπττει από τον
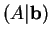
εφαρμόζοντας ένα στοιχειώδη μετασχηματισμό γραμμών τότε
τα συστήματα
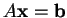
και
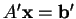
είναι ισοδύναμα.
Πόρισμα 3
Ένα σύστημα της μορφής
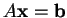
μπορεί να λυθεί αν βρούμε την
αναγμένη μορφή του επαυξημένου πίνακα του συστήματος. Η παραπάνω
μέθοδος λύσης λέγεται απαλοιφή του Gauss.
Θεώρημα 14
Έστω

ένα σώμα και
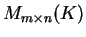
το σύνολο των
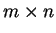
πινάκων
με στοιχεία στο

.
Τότε το
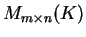
είναι ένας διανυσματικός
χώρος στο

.
Ορισμός 19
Αν
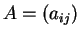
ένας
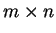
πίνακας τότε ο πίνακας
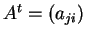
λέγεται ανάστροφος του

.
Ένας πίνακας λέγεται τετραγωνικός αν 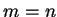 .
.
Άν 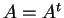 τότε ο
τότε ο  λέγεται συμμετρικός. Ένας συμμετρικός πίνακας είναι
τετραγωνικός.
λέγεται συμμετρικός. Ένας συμμετρικός πίνακας είναι
τετραγωνικός.
Ο πίνακας
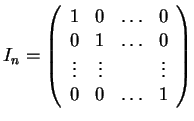 λέγεται μοναδιαίος
λέγεται μοναδιαίος 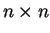 πίνακας.
πίνακας.
Ένας πίνακας  λέγεται μηδενοδύναμος αν υπάρχει ακέραιος
λέγεται μηδενοδύναμος αν υπάρχει ακέραιος
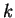 ώστε
ώστε 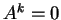 .
.
Θεώρημα 15
Έστω
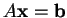
ένα σύστημα γραμμικών εξισώσεων με

έναν τετραγωνικό πίνακα
διάστασης
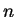
.
Aν τα διανύσματα
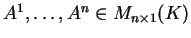
είναι γραμμικώς ανεξάρτητα τότε το σύστημα έχει μοναδική λύση στο

.
Ορισμός 20
Ένας
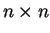
πίνακας λέγεται στοιχειώδης πίνακας αν μπορεί να προκύψει
από τον
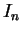
εφαρμόζοντας ένα στοιχειώδη μετασχηματισμό γραμμών.
Θεώρημα 16
Ένας
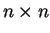
πίνακας

είναι είναι αντιστρέψιμος αν και μόνο αν
είναι το γινόμενο στοιχειωδών πινάκων.
Πόρισμα 4
Aν

αντιστρέψιμος πίνακας τότε ο
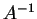
ορίζεται εφαρμόζοντας τους
ίδιους στοιχειώδεις μετασχηματισμούς γραμμών στον
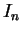
που εφαρμόζουμε
στον

για να πάρουμε τον
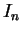
.



Next: Άσκηση 26
Up: Γραμμικά Συστήματα και Πίνακες
Previous: Γραμμικά Συστήματα και Πίνακες
Vassilis Metaftsis
1999-09-15
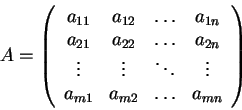
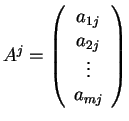 για κάθε
για κάθε 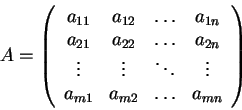
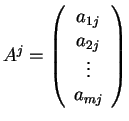 για κάθε
για κάθε 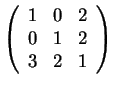 είναι γραμμοϊσοδύναμος με τον πίνακα
είναι γραμμοϊσοδύναμος με τον πίνακα
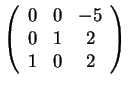 εφόσον
εφόσον
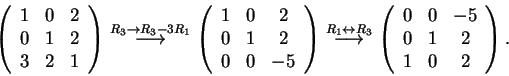
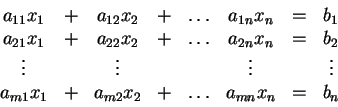
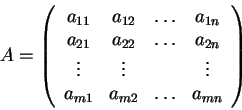
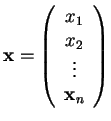 και
και
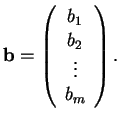 To σύστημα
To σύστημα 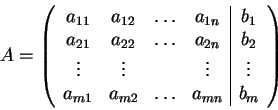
![]() .
.
![]() τότε ο
τότε ο ![]() λέγεται συμμετρικός. Ένας συμμετρικός πίνακας είναι
τετραγωνικός.
λέγεται συμμετρικός. Ένας συμμετρικός πίνακας είναι
τετραγωνικός.
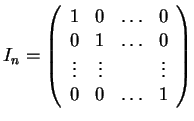 λέγεται μοναδιαίος
λέγεται μοναδιαίος ![]() πίνακας.
πίνακας.
![]() λέγεται μηδενοδύναμος αν υπάρχει ακέραιος
λέγεται μηδενοδύναμος αν υπάρχει ακέραιος
![]() ώστε
ώστε ![]() .
.