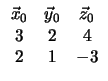Έστω x0 = 1, αντικαθιστούμε στις εξισώσεις που ορίζουν την ευθεία και
βρίσκουμε
y0 = 2, z0 = 1. Το διάνυσμα
![]() = (3, 2, 4) είναι κάθετο στο
επίπεδο
3x + 2y + 4z - 11 = 0 και το διάνυσμα
= (3, 2, 4) είναι κάθετο στο
επίπεδο
3x + 2y + 4z - 11 = 0 και το διάνυσμα
![]() = (2, 1, - 3) είναι κάθετο
στο επίπεδο
2x + y - 3z - 1 = 0. Η ευθεία
(
= (2, 1, - 3) είναι κάθετο
στο επίπεδο
2x + y - 3z - 1 = 0. Η ευθεία
(![]() ) ως κοινή ευθεία των δύο επιπέδων
είναι κάθετη και στα δύο διανύσματα
) ως κοινή ευθεία των δύο επιπέδων
είναι κάθετη και στα δύο διανύσματα
![]() ,
, ![]() , και άρα παράλληλη
στο διάνυσμα
, και άρα παράλληλη
στο διάνυσμα