

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Τα κέντρα και οι ακτίνες των δύο περιφερειών είναι
Ki(-
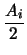
, -
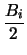
),
Ri =
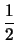
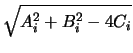
,
i = 1, 2.
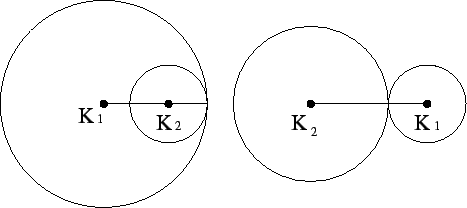
Συνεπώς α) για να εφάπτονται εσωτερικά θα πρέπει
|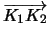 | = | R1 - R2|, και άρα
| = | R1 - R2|, και άρα
4
R1R2 =
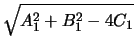
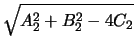
=
A1A2 +
B1B2 - 2
C1 - 2
C2,
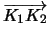 | = R1 + R2, και άρα
| = R1 + R2, και άρα
4
R1R2 =
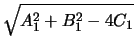
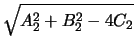
= 2
C1 + 2
C2 -
A1A2 -
B1B2.
Aristophanes Dimakis
1999-10-05
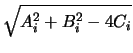 , i = 1, 2.
, i = 1, 2.
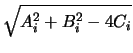 , i = 1, 2.
, i = 1, 2.

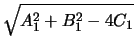
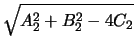 = A1A2 + B1B2 - 2C1 - 2C2,
= A1A2 + B1B2 - 2C1 - 2C2,
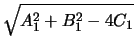
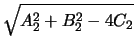 = 2C1 + 2C2 - A1A2 - B1B2.
= 2C1 + 2C2 - A1A2 - B1B2.