

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Έστω ότι η ζητούμενη περιφέρεια είναι
(x - 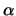 )2 + (y -
)2 + (y - 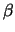 )2 = R2.
)2 = R2.
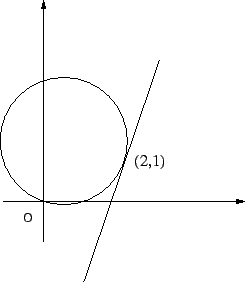
Επειδή η αρχή των αξόνων -- το σημείο (0,0) -- βρίσκεται πάνω στην περιφέρεια,
έχουμε
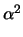 +
+ 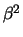 = R2. Η εξίσωση της εφαπτομένης στο σημείο (2,1)
είναι
= R2. Η εξίσωση της εφαπτομένης στο σημείο (2,1)
είναι
(2 -
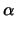
)(
x -
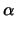
) + (1 -
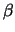
)(
y -
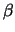
) =
R2 =
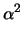
+
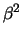
.
(2 -
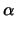
)
x + (1 -
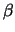
)
y - (2
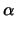
+
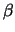
) = 0.
Aristophanes Dimakis
1999-10-05
![]() )2 + (y -
)2 + (y - ![]() )2 = R2.
)2 = R2.

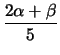 .
.