

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Έστω
(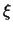 ,
,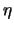 ) τυχαίο σημείο της ευθείας
(
) τυχαίο σημείο της ευθείας
(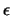 ). Ηπολική ευθεία του
σημείου αυτού ως προς την (C) είναι
). Ηπολική ευθεία του
σημείου αυτού ως προς την (C) είναι
Τα σημεία τομής της πολικής με την (C) είναι τα ακρα της χορδής. Λύνουμε
το σύστημα των
(C), (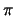 ) και βρίσκουμε
Αν x1, x2 είναι η ρίζες αυτής της εξίσωσης, τοτε η x-συντεταγμένη του
μέσου της χορδής είναι
x0 = (x1 + x2)/2. Έχουμε λοιπόν
) και βρίσκουμε
Αν x1, x2 είναι η ρίζες αυτής της εξίσωσης, τοτε η x-συντεταγμένη του
μέσου της χορδής είναι
x0 = (x1 + x2)/2. Έχουμε λοιπόν
x0 =
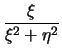
,
y0 =
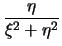
.
Λύνουμε ως προς
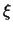 ,
, 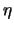 Επειδή το σημείο
Επειδή το σημείο 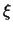 ,
,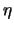 ) ανήκει στην
(
) ανήκει στην
(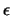 ) αντικαθιστούμε στην
εξίσωση της ευθείας και παίρνουμε
) αντικαθιστούμε στην
εξίσωση της ευθείας και παίρνουμε
3
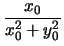
+ 4
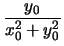
+ 6 = 0
Aristophanes Dimakis
1999-10-05
![]() ,
,![]() ) τυχαίο σημείο της ευθείας
(
) τυχαίο σημείο της ευθείας
(![]() ). Ηπολική ευθεία του
σημείου αυτού ως προς την (C) είναι
). Ηπολική ευθεία του
σημείου αυτού ως προς την (C) είναι
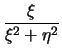 , y0 =
, y0 =