next up previous
Next: Άσκηση Up: Άσκηση Previous: Υπόδειξη

Λύση

Η γενική εξίσωση της περιφέρειας με κέντρο K(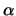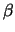$ \alpha$,$ \beta$) και ακτίνα R είναι

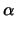
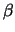
(x - $\displaystyle \alpha$)2 + (y - $\displaystyle \beta$)2 = R2.

α) Όπως φαίνεται από το σχήμα
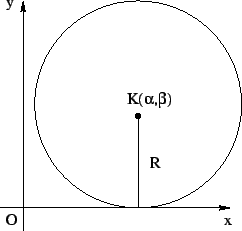
\epsfig{file=ask57.eps, scale=.8}
όταν η περιφέρεια εφάπτεται στον άξονα Ox η y-συντεταγμένη του κέντρου της περιφέρειας σε απόλυτη τιμή ισούται με την ακτίνα. Συνεπώς η γενική εξίσωση μιας περιφέρειας που εφάπτεται στον άξονα Ox είναι

(x - $\displaystyle \alpha$)2 + (y - $\displaystyle \beta$)2 = $\displaystyle \beta^{2}_{}$.

Ανάλογα βρίσκουμε για την περίπτωση β)

(x - $\displaystyle \alpha$)2 + (y - $\displaystyle \beta$)2 = $\displaystyle \alpha^{2}_{}$,

και για την περίπτωση γ)

(x - $\displaystyle \alpha$)2 + (y$\displaystyle \pm$$\displaystyle \alpha$)2 = $\displaystyle \alpha^{2}_{}$.


Aristophanes Dimakis
1999-10-05