

Next: About this document ...
Up: Άσκηση
Previous: Υπόδειξη
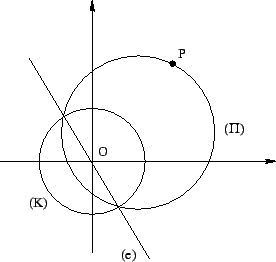
Έστω
x2 + y2 + Ax + By + C = 0 μια των περιφερειών ( ) που ενδιαφέρουν. Τα κοινα
σημεία αυτής με την (K) βρίσκονται πάνω στην ευθεία
(
) που ενδιαφέρουν. Τα κοινα
σημεία αυτής με την (K) βρίσκονται πάνω στην ευθεία
( )
)
(x2 + y2 + Ax + By + C) - (x2 + y2 - R2) = Ax + By + C + R2 = 0.
Η ευθεία
(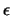 ) επειδή τέμνει την (K) στα άκρα διαμέτρου διέρχεται από
το κέντρο του (K) που είναι η αρχή των αξόνων O(0, 0). Άρα έχουμε
) επειδή τέμνει την (K) στα άκρα διαμέτρου διέρχεται από
το κέντρο του (K) που είναι η αρχή των αξόνων O(0, 0). Άρα έχουμε
A0 +
B0 +
C +
R2 = 0
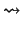 C
C = -
R2.
Οι περιφέρειες (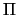 ) διέρχονται από το σημείο
P(
) διέρχονται από το σημείο
P(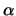 ,
,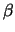 ), συνεπώς
Αν (x0, y0) οι συντεταγμένες των κέντρων των (
), συνεπώς
Αν (x0, y0) οι συντεταγμένες των κέντρων των (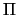 ), τότε A = - 2x0 και
B = - 2y0. Αντικαθιστούμε στην παραπάνω και βρίσκουμε ότι τα κέντρα των (
), τότε A = - 2x0 και
B = - 2y0. Αντικαθιστούμε στην παραπάνω και βρίσκουμε ότι τα κέντρα των (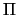 )
ικανοποιούν την εξίσωση
Συνεπώς ο ζητούμενος γεωμετρικός τόπος είναι η ευθεία
)
ικανοποιούν την εξίσωση
Συνεπώς ο ζητούμενος γεωμετρικός τόπος είναι η ευθεία
Aristophanes Dimakis
1999-10-05
![]() ) που ενδιαφέρουν. Τα κοινα
σημεία αυτής με την (K) βρίσκονται πάνω στην ευθεία
(
) που ενδιαφέρουν. Τα κοινα
σημεία αυτής με την (K) βρίσκονται πάνω στην ευθεία
(![]() )
)
