β) Η εξίσωση παίρνει τη μορφή
α) Έχουμε
A = a2 - 3a + 2 = 0, άν a = 1 ή a = 2. Όμοια
B = 2a2 - a - 1 = 0, αν
a = 1 ή a = - 1/2. Άρα γιά να έχουμε ευθεία πρέπει a ![]() 1.
1.
β) Η εξίσωση παίρνει τη μορφή
| a2(x + 2y - 3) + a(- 3x - y + 4) + (2x - y - 1) = 0. |
| x + 2y - 3 = 0, - 3x - y + 4 = 0, 2x - y - 1 = 0, |
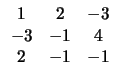
|