D = 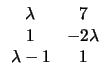
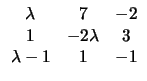
|
Έχουμε
D = 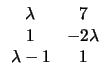
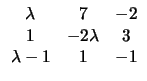
|
Η ορίζουσα του E είναι
-2(![]() - 11
- 11![]() + 8) που μηδενίζεται στίς
τιμές
+ 8) που μηδενίζεται στίς
τιμές
![]() =
= ![]() . Συνεπώς γιά
. Συνεπώς γιά
![]()
![]()
![]() οι τρείς ευθείες είναι σε γενική θεση, δηλ. σχηματίζουν ένα τρίπλευρο. Για
οι τρείς ευθείες είναι σε γενική θεση, δηλ. σχηματίζουν ένα τρίπλευρο. Για
![]() = 7/6 η πρώτη και η τρίτη είναι
παράλληλες. Γιά
= 7/6 η πρώτη και η τρίτη είναι
παράλληλες. Γιά
![]() =
= ![]() έχουμε r(E) = 2 και οι τρείς
ευθείες έχουν ένα κοινό σημείο.
έχουμε r(E) = 2 και οι τρείς
ευθείες έχουν ένα κοινό σημείο.