

Next: Άσκηση
Up: Ασκηση
Previous: Υπόδειξη
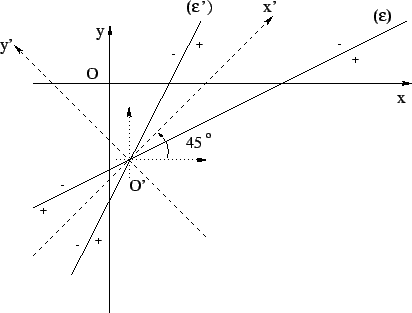
Το σημείο τομής των
(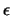 ), (
), (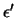 ) είναι το O'(1, - 4). Επειδή
τα σημεία των διχοτόμων ισαπέχουν από τις πλευρες των γωνιών έχουμε
) είναι το O'(1, - 4). Επειδή
τα σημεία των διχοτόμων ισαπέχουν από τις πλευρες των γωνιών έχουμε
Από εδώ παίρνουμε γιά τον O'x': x - y - 5 = 0 και γιά τον O'y': x + y + 3 = 0.
Η αλλαγή των συντεταγμένων είναι
| x |
= |
1 + x'cos 45o - y'sin 45o = 1 + 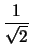 (x' - y') (x' - y') |
|
| y |
= |
-4 + x'sin 45o + y'cos 45o = - 4 + 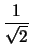 (x' + y'). (x' + y'). |
|
Αντικαθιστώντας στις εξισώσεις των ευθειών παίρνουμε για την
(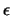 ):
x' + 3y' = 0 και γιά την
(
):
x' + 3y' = 0 και γιά την
(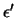 ): x' - 3y' = 0.
): x' - 3y' = 0.
Aristophanes Dimakis
1999-10-05

![]() ), (
), (![]() ) είναι το O'(1, - 4). Επειδή
τα σημεία των διχοτόμων ισαπέχουν από τις πλευρες των γωνιών έχουμε
) είναι το O'(1, - 4). Επειδή
τα σημεία των διχοτόμων ισαπέχουν από τις πλευρες των γωνιών έχουμε
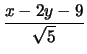 =
= 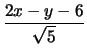 .
.