

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Το (E) ανήκει στην δέσμη με άξονα την ευθεία
(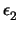 ), άρα έχει εξίσωση
της μορφής
), άρα έχει εξίσωση
της μορφής
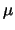
(3
x + 2
y + 5
z + 6) +
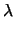
(
x + 4
y + 3
z + 4) = 0
συνεπώς
(3
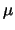
+
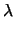
)
x + (2
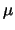
+ 4
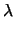
)
y + (5
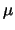
+ 3
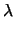
)
z + (6
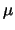
+ 4
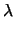
) = 0
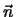 = (3
= (3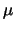 +
+ 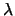 , 2
, 2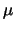 + 4
+ 4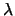 , 5
, 5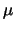 + 3
+ 3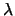 )
είναι κάθετο στο ζητούμενο επίπεδο και άρα κάθετο προς το διάνυσμα
)
είναι κάθετο στο ζητούμενο επίπεδο και άρα κάθετο προς το διάνυσμα
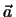 = (3, 2, - 3), που είναι παράλληλο προς την ευθεία
(
= (3, 2, - 3), που είναι παράλληλο προς την ευθεία
(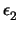 ).
).
Έχουμε λοιπόν
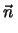 .
. 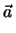
= 0
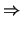
3(3
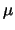
+
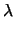
) + 2(5
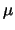
+ 3
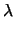
) - 3(6
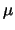
+ 4
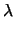
) = 0
από όπου παίρνουμε
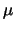 =
= 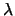 και συνεπώς
και συνεπώς
(E) : 2x + 3y + 4z + 5 = 0.
Aristophanes Dimakis
1999-10-05
![]() ), άρα έχει εξίσωση
της μορφής
), άρα έχει εξίσωση
της μορφής