Στοιχεία Θεωρίας

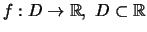
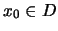
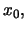
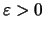
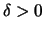
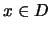
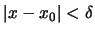
Ορισμός 37   'Εστω συνάρτηση $f : D \rightarrow \mathbb R, \; D \subset \mathbb R$ και $x_0 \in D$. Η $f$ λέγεται συνεχής στο $x_0,$ αν για κάθε $\varepsilon >0$ υπάρχει $\delta > 0$ τέτοιο ώστε για κάθε $x \in D$ με $\vert x - x_0\vert < \delta$ να έχουμε $\vert f(x) - f(x_0)\vert < \varepsilon.$

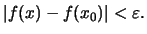
Θεώρημα 38   Το άθροισμα, η διαφορά, το γινόμενο, το πηλίκο και η σύνθεση συνεχών συναρτήσεων, (στο πεδίο ορισμού όπου αυτές ορίζονται), είναι συνεχείς συναρτήσεις.

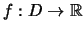
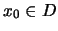
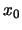
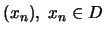
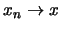
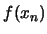
Θεώρημα 39 (Heine)   'Εστω συνάρτηση $f : D \rightarrow \mathbb R$ και $x_0 \in D$. Η $f$ είναι συνεχής στο $x_0$ αν και μόνο αν για κάθε ακολουθία $(x_n),\; x_n \in D$ με $x_n \to x$ η ακολουθία $f(x_n)$ συγκλίνει στο $f(x_0)$.

Ορισμός 40   Αν μια συνάρτηση $f$ δεν είναι συνεχής σε ένα σημείο $x_0$, τότε μπορεί να συμβεί ένα από τα ακόλουθα τρία ενδεχόμενα.

(i) $f(x_0^+) = f(x_0^-) \not =f(x_0)$ και λέμε ότι η $f$ έχει άρσιμη ασυνέχεια στο σημείο $x_0$.

(ii) $f(x_0^+) \not = f(x_0^-)$ και λέμε ότι η $f$ έχει ασυνέχεια α' είδους ή πήδημα στο σημείο $x_0$.

(iii) Τουλάχιστον ένα από τα δύο πλευρικά όρια δεν υπάρχει και λέμε ότι η $f$ έχει ασυνέχεια β' είδους ή ουσιώδη ασυνέχεια στο σημείο $x_0$.

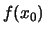
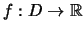
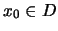
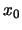
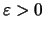
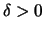
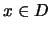
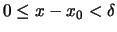
Ορισμός 41   'Εστω συνάρτηση $f : D \rightarrow \mathbb R$ και $x_0 \in D$. Η $f$ λέγεται συνεχής από τα δεξιά στο $x_0$, αν για κάθε $\varepsilon >0$ υπάρχει $\delta > 0$ τέτοιο ώστε για κάθε $x \in D$ με $0 \leq x - x_0 < \delta$ να έχουμε $\vert f(x) - f(x_0)\vert < \varepsilon.$

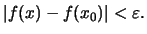
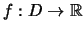
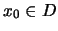
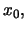
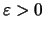
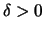
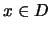
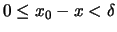
Ορισμός 42   'Εστω συνάρτηση $f : D \rightarrow \mathbb R$ και $x_0 \in D$. Η $f$ λέγεται συνεχής από τα αριστερά στο $x_0,$ αν για κάθε $\varepsilon >0$ υπάρχει $\delta > 0$ τέτοιο ώστε για κάθε $x \in D$ με $0 \leq x_0 - x < \delta$ να έχουμε $\vert f(x) - f(x_0)\vert < \varepsilon.$

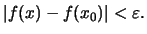
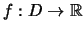
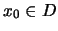
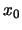
Θεώρημα 43   'Εστω συνάρτηση $f : D \rightarrow \mathbb R$ και $x_0 \in D$. Η $f$ είναι συνεχής στο $x_0$, αν και μόνον αν είναι συνεχής από δεξιά και από αριστερά στο $x_0$.

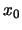
Θεώρημα 44   'Εστω $f : [a,b] \rightarrow \mathbb R$ συνεχής συνάρτηση. Τότε

(i) H $f$ είναι φραγμένη στο διάστημα $[a,b]$.

(ii) Υπάρχει $x_0 \in [a,b]$ τέτοιο ώστε

$$f(x_0) = \sup \{f(x), \; a\leq x \leq b \}.$$

'Ολες οι προ"υποθέσεις του θεωρήματος είναι απαραίτητες.

Πόρισμα 45   'Εστω $f : [a,b] \rightarrow \mathbb R$ συνεχής συνάρτηση. Τότε υπάρχει $x_1 \in [a,b]$ τέτοιο ώστε

$$f(x_1) = \inf \{f(x), \; a\leq x \leq b \}.$$

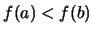
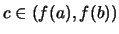
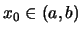
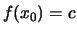
Θεώρημα 46 (Ενδιάμεσης τιμής)   'Εστω $f : [a,b] \rightarrow \mathbb R$ συνεχής συνάρτηση με $f(a) < f(b)$ και $c\in (f(a), f(b))$. Τότε υπάρχει $x_0 \in (a,b)$ τέτοιο ώστε $f(x_0) = c$. Ανάλογο συμπέρασμα ισχύει και για $f(a) > f(b).$

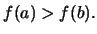
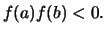
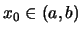
Θεώρημα 47 (Bolzano - Weierstrass)   'Εστω $f : [a,b] \rightarrow \mathbb R$ συνεχής συνάρτηση με $f(a) f(b) < 0.$ Τότε υπάρχει $x_0 \in (a,b)$ τέτοιο ώστε $f(x_0) = 0$.

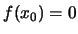
Παρατήρηση. Τα Θεωρήματα ενδιάμεσης τιμής και Bolzano - Weierstrass είναι ισοδύναμα.