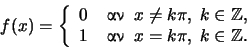Next: 'Ασκηση 6
Up: 'Ασκηση 5
Previous: Υπόδειξη
Λύση
Για
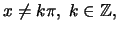 είναι
είναι 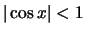 ,
οπότε από τα όρια ακολουθιών
έχουμε ότι
,
οπότε από τα όρια ακολουθιών
έχουμε ότι
Για
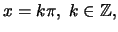 έχουμε
έχουμε 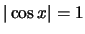 και άρα
και άρα
Οπότε έχουμε
Επειδή
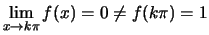 έχουμε ότι στα σημεία
έχουμε ότι στα σημεία
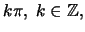 η συνάρτηση δεν είναι συνεχής
και μάλιστα έχει άρσιμη ασυνέχεια. Στα υπόλοιπα σημεία είναι φανερό ότι είναι
συνεχής.
η συνάρτηση δεν είναι συνεχής
και μάλιστα έχει άρσιμη ασυνέχεια. Στα υπόλοιπα σημεία είναι φανερό ότι είναι
συνεχής.
'Ασκηση 5
Υπόδειξη
Antonis Tsolomitis
1999-11-11
![]() έχουμε
έχουμε ![]() και άρα
και άρα