Next: 'Ασκηση 5
Up: 'Ασκηση 4
Previous: Υπόδειξη
Λύση
'Εστω
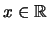 .
Η
.
Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο
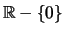 με
με
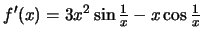 .
Εξετάζουμε την παραγωγισιμότητα στο
.
Εξετάζουμε την παραγωγισιμότητα στο 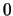 με τη βοήθεια του ορισμού. 'Εχουμε
με τη βοήθεια του ορισμού. 'Εχουμε
αφού
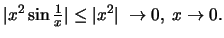 Άρα η συνάρτηση είναι παραγωγίσιμη
στο
Άρα η συνάρτηση είναι παραγωγίσιμη
στο 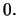 Τελικά έχουμε
Τελικά έχουμε
Από τη σχέση αυτή έχουμε ότι η 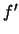 είναι συνεχής για
είναι συνεχής για
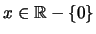 .
Στο σημείο
.
Στο σημείο
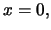 η
η 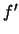 είναι επίσης συνεχής αφού
είναι επίσης συνεχής αφού
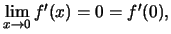 όπως εύκολα μπορεί κανείς να διαπιστώσει.
όπως εύκολα μπορεί κανείς να διαπιστώσει.
'Ασκηση 4
Υπόδειξη
Antonis Tsolomitis
1999-11-11