


Next: 'Ασκηση 15
Up: 'Ασκηση 14
Previous: Υπόδειξη
Λύση
Αν 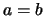 τότε η ανισότητα είναι φανερή. Στη συνέχεια υποθέτουμε ότι
τότε η ανισότητα είναι φανερή. Στη συνέχεια υποθέτουμε ότι 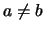 και
χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι
και
χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι 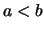 (γιατί;).
Θεωρούμε τη συνάρτηση
(γιατί;).
Θεωρούμε τη συνάρτηση
![$f : [a,b] \rightarrow \mathbb R$](img432.gif) με
με 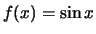 .
Η
.
Η  είναι συνεχής στο
είναι συνεχής στο ![$[a,b]$](img433.gif) και παραγωγίσιμη στο
και παραγωγίσιμη στο 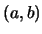 .
Από το θεώρημα μέσης τιμής
έχουμε ότι υπάρχει
.
Από το θεώρημα μέσης τιμής
έχουμε ότι υπάρχει
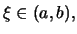 τέτοιο ώστε
τέτοιο ώστε
και άρα
Από εδώ προκύπτει η ζητούμενη ανισότητα.
'Ασκηση 14
Υπόδειξη
Antonis Tsolomitis
1999-11-11