


Next: 'Ασκηση 16
Up: 'Ασκηση 15
Previous: Υπόδειξη
Λύση
'Εστω 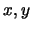 οι διαστάσεις του ορθογωνίου με εμβαδόν
οι διαστάσεις του ορθογωνίου με εμβαδόν 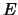 .
Τότε ισχύει
.
Τότε ισχύει 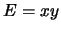 .
Αν
.
Αν
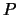 η περίμετρος του ορθογωνίου, έχουμε
η περίμετρος του ορθογωνίου, έχουμε
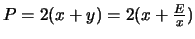 .
Θεωρούμε τη
συνάρτηση
.
Θεωρούμε τη
συνάρτηση
Επειδή
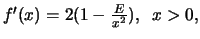 έχουμε
έχουμε
Οπότε η  είναι αύξουσα στο
είναι αύξουσα στο
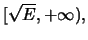 φθίνουσα στο
φθίνουσα στο ![$(0, \sqrt E]$](img774.gif) και άρα στο
και άρα στο
έχει ολικό ελάχιστο.
Δηλαδή το ορθογώνιο είναι τετράγωνο.
'Ασκηση 15
Υπόδειξη
Antonis Tsolomitis
1999-11-11