


Next: 'Ασκηση 17
Up: 'Ασκηση 16
Previous: Υπόδειξη
Λύση
Παραγωγίζοντας έχουμε
Για
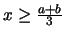 είναι
είναι 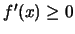 και άρα στο διάστημα
και άρα στο διάστημα
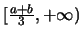 η
συνάρτηση είναι αύξουσα ενώ για
η
συνάρτηση είναι αύξουσα ενώ για
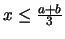 είναι
είναι 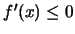 και άρα στο
διάστημα
και άρα στο
διάστημα
![$(-\infty, \frac{a+b}{3}]$](img784.gif) η συνάρτηση είναι φθίνουσα. Οπότε στο σημείο
η συνάρτηση είναι φθίνουσα. Οπότε στο σημείο
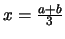 η συνάρτηση έχει ολικό ελάχιστο, ίσο με
η συνάρτηση έχει ολικό ελάχιστο, ίσο με
'Ασκηση 16
Υπόδειξη
Antonis Tsolomitis
1999-11-11