


Next: 'Ασκηση 18
Up: 'Ασκηση 17
Previous: Υπόδειξη
Λύση
Από τις σχέσεις 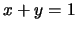 και
και 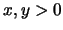 έχουμε ότι
έχουμε ότι 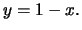 Θεωρούμε τη συνάρτηση
Θεωρούμε τη συνάρτηση
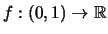 με
με
'Εχουμε
Είναι
οπότε η  είναι αύξουσα στο
είναι αύξουσα στο
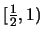 και φθίνουσα στο
και φθίνουσα στο
![$(0, \frac{1}{2}].$](img798.gif) Άρα στο
Άρα στο 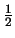 έχει ολικό ελάχιστο, δηλαδή
έχει ολικό ελάχιστο, δηλαδή
Θέτοντας 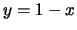 έχουμε τη ζητούμενη ανισότητα.
έχουμε τη ζητούμενη ανισότητα.
'Ασκηση 17
Υπόδειξη
Antonis Tsolomitis
1999-11-11