


Next: 'Ασκηση 21
Up: 'Ασκηση 20
Previous: Υπόδειξη
Λύση
Θεωρούμε την συνάρτηση
(η οποία είναι καλώς ορισμένη). Επειδή
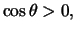 έχουμε
έχουμε
για
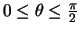 και
και 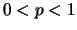 αφού
αφού
![$ \sin[(p-1)\theta] < 0$](img833.gif) .
Σύμφωνα με γνωστό θεώρημα η
.
Σύμφωνα με γνωστό θεώρημα η 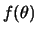 είναι φθίνουσα και άρα
είναι φθίνουσα και άρα
Από τη σχέση αυτή προκύπτει η ζητούμενη σχέση άμεσα.
'Ασκηση 20
Υπόδειξη
Antonis Tsolomitis
1999-11-11
![\begin{eqnarray*}
f'(\theta) &= & \frac{p (\cos \theta)^{p-1}}{\cos^2(p\theta)}[...
...ac{p (\cos \theta)^{p-1}}{\cos^2(p\theta)} \sin[(p-1)\theta] < 0
\end{eqnarray*}](img831.gif)