Λύση

Είναι φανερό πως το όριο δεν υπολογίζεται με τη χρήση των ιδιοτήτων των ορίων. Tο μετασχηματίζουμε κατάληλα, ώστε να μπορέσουμε να εφαρμόσουμε τον κανόνα του L' Hospital. Είναι

$$x \log \left (\frac{x+1}{x-1}\right) = \frac {\log \left (\frac{x+1} {x-1}\right)}{\frac{1}{x}}$$

και αυτή η μορφή είναι απροσδιοριστία για 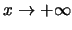$x \to +\infty$ της μορφής 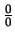$\frac{0}{0}$. Έχουμε

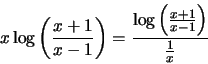
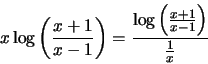
$$\frac {\left[\log \left (\frac{x+1}{x-1}\right)\right]'} {(\frac{1}{x})'} = \frac{2x^2}{x^2 - 1} \to 2, \; x \to +\infty.$$

Οπότε, σύμφωνα με τον κανόνα του L' Hospital είναι

$$\lim\limits_{x \to +\infty}x \log \left (\frac{x+1}{x-1}\right) = 2.$$

'Ασκηση 26 Υπόδειξη