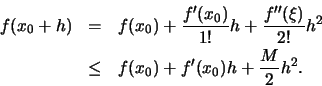Next: About this document ...
Up: 'Ασκηση 30
Previous: Υπόδειξη
Λύση
Από τον τύπο του Taylor έχουμε ότι
για
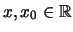 και
και 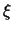 μεταξύ των
μεταξύ των 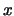 και
και 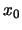 .
Θέτοντας
.
Θέτοντας 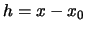 και επειδή
και επειδή
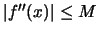 ,
έχουμε
,
έχουμε
Λόγω της σχέσης 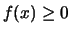 για κάθε
για κάθε
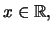 το τριώνυμο
το τριώνυμο
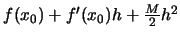 πρέπει να είναι θετικό για κάθε
πρέπει να είναι θετικό για κάθε
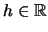 και άρα η διακρίνουσά του να είναι αρνητική. Δηλαδή
και άρα η διακρίνουσά του να είναι αρνητική. Δηλαδή
Επειδή το 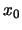 είναι τυχαίο σημείο του
είναι τυχαίο σημείο του 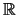 έχουμε τη ζητούμενη σχέση.
έχουμε τη ζητούμενη σχέση.
'Ασκηση 30
Υπόδειξη
Antonis Tsolomitis
1999-11-11