


Next: 'Ασκηση 2
Up: 'Ασκηση 1
Previous: Υπόδειξη
Λύση
Από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι για κάθε
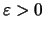 υπάρχει φυσικός
υπάρχει φυσικός 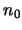 τέτοιος ώστε
τέτοιος ώστε
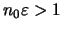 ,
δηλαδή
,
δηλαδή
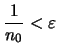 .
Αν
.
Αν
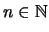 με
με 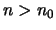 τότε
τότε
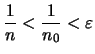 και άρα για κάθε
και άρα για κάθε
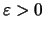 ,
υπάρχει φυσικός
,
υπάρχει φυσικός 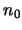 ,
τέτοιος ώστε αν
,
τέτοιος ώστε αν
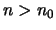 να έχουμε
να έχουμε
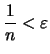 .
Σύμφωνα όμως με τον ορισμό της
σύγκλισης ακολουθιών αυτό σημαίνει ότι
.
Σύμφωνα όμως με τον ορισμό της
σύγκλισης ακολουθιών αυτό σημαίνει ότι
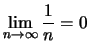 .
.
'Ασκηση 1
Υπόδειξη
Antonis Tsolomitis
1999-11-11
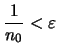 .
Αν
.
Αν
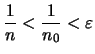 και άρα για κάθε
και άρα για κάθε
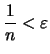 .
Σύμφωνα όμως με τον ορισμό της
σύγκλισης ακολουθιών αυτό σημαίνει ότι
.
Σύμφωνα όμως με τον ορισμό της
σύγκλισης ακολουθιών αυτό σημαίνει ότι
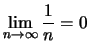 .
.