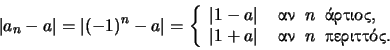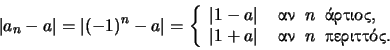Next: 'Ασκηση 3
Up: 'Ασκηση 2
Previous: Υπόδειξη
Λύση
Έστω ότι η ακολουθία συγκλίνει στο 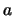 .
Τότε σύμφωνα με τον ορισμό έχουμε ότι για
κάθε
.
Τότε σύμφωνα με τον ορισμό έχουμε ότι για
κάθε
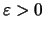 υπάρχει
υπάρχει
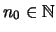 τέτοιο ώστε, για κάθε
τέτοιο ώστε, για κάθε
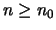 να έχουμε
να έχουμε
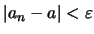 .
'Ομως
.
'Ομως
Άρα
ή ισοδύναμα
και άρα
Οπότε
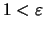 που είναι άτοπο, αφού το
που είναι άτοπο, αφού το 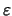 είναι τυχαίος θετικός αριθμός.
είναι τυχαίος θετικός αριθμός.
'Ασκηση 2
Υπόδειξη
Antonis Tsolomitis
1999-11-11