


Next: 'Ασκηση 4
Up: 'Ασκηση 3
Previous: Υπόδειξη
Λύση
Θα δείξουμε ότι η ακολουθία συγκλίνει στο 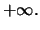 Αν δεν συνέκλινε στο
Αν δεν συνέκλινε στο 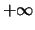 τότε, από την άρνηση του ορισμού, έχουμε ότι υπάρχει
τότε, από την άρνηση του ορισμού, έχουμε ότι υπάρχει
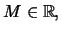 για κάθε
για κάθε
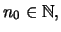 θα υπάρχει
θα υπάρχει 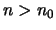 τέτοιο ώστε να έχουμε
τέτοιο ώστε να έχουμε 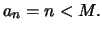 Παίρνοντας
Παίρνοντας
![$n_0 = [\vert M\vert] +1$](img225.gif) έχουμε ότι υπάρχει
έχουμε ότι υπάρχει
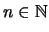 με
με 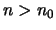 ώστε να έχουμε
ώστε να έχουμε
που σύμφωνα με τον ορισμό του ακεραίου μέρους είναι άτοπο.
'Ασκηση 3
Υπόδειξη
Antonis Tsolomitis
1999-11-11