


Next: 'Ασκηση 2
Up: 'Ασκηση 1
Previous: Υπόδειξη
Λύση
(Εύδοξος) Υποθέτουμε ότι
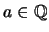 .
Τότε υπάρχουν
.
Τότε υπάρχουν
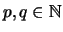 τέτοιοι ώστε
τέτοιοι ώστε
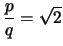 και οι οποίοι δεν διαιρούνται ταυτόχρονα με το 2.
Επειδή
και οι οποίοι δεν διαιρούνται ταυτόχρονα με το 2.
Επειδή
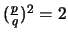 έχουμε ότι
έχουμε ότι
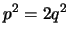 ,
άρα ο
,
άρα ο 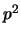 είναι άρτιος,
οπότε και ο
είναι άρτιος,
οπότε και ο 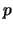 θα είναι άρτιος, έστω
θα είναι άρτιος, έστω 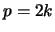 .
Αντικαθιστώντας έχουμε ότι
.
Αντικαθιστώντας έχουμε ότι
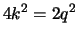 ,
άρα
,
άρα
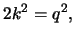 οπότε ο
οπότε ο 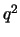 είναι άρτιος, άρα και ο
είναι άρτιος, άρα και ο
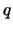 θα είναι άρτιος. Άτοπο αφού υποθέσαμε ότι οι
θα είναι άρτιος. Άτοπο αφού υποθέσαμε ότι οι 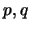 δεν διαιρούνται ταυτόχρονα
με το 2.
δεν διαιρούνται ταυτόχρονα
με το 2.
'Ασκηση
Υπόδειξη
Antonis Tsolomitis
1999-11-11