


Next: 'Ασκηση 14
Up: 'Ασκηση 13
Previous: Υπόδειξη
Λύση
Αρκεί να δείξουμε ότι η 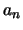 δεν είναι ακολουθία Cauchy. Eλέγχουμε τη
διαφορά
δεν είναι ακολουθία Cauchy. Eλέγχουμε τη
διαφορά
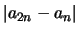 .
Έχουμε
.
Έχουμε
Από την ανισότητα αυτή προκύπτει ότι η 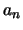 δεν είναι
Cauchy και άρα σύμφωνα με γνωστό θεώρημα δεν συγκλίνει.
δεν είναι
Cauchy και άρα σύμφωνα με γνωστό θεώρημα δεν συγκλίνει.
Παρατήρηση.
Από τη σχέση
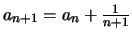 έχουμε ότι η ακολουθία μας είναι αύξουσα.
Επειδή όπως είδαμε, δεν συγκλίνει συμπεραίνουμε ότι δεν είναι φραγμένη (αν ήταν θα
έπρεπε να συγκλίνει - σύμφωνα με γνωστό θεώρημα) και άρα
συγκλίνει στο
έχουμε ότι η ακολουθία μας είναι αύξουσα.
Επειδή όπως είδαμε, δεν συγκλίνει συμπεραίνουμε ότι δεν είναι φραγμένη (αν ήταν θα
έπρεπε να συγκλίνει - σύμφωνα με γνωστό θεώρημα) και άρα
συγκλίνει στο 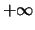 ,
(γιατί;).
,
(γιατί;).
'Ασκηση 13
Υπόδειξη
Antonis Tsolomitis
1999-11-11
![]() έχουμε ότι η ακολουθία μας είναι αύξουσα.
Επειδή όπως είδαμε, δεν συγκλίνει συμπεραίνουμε ότι δεν είναι φραγμένη (αν ήταν θα
έπρεπε να συγκλίνει - σύμφωνα με γνωστό θεώρημα) και άρα
συγκλίνει στο
έχουμε ότι η ακολουθία μας είναι αύξουσα.
Επειδή όπως είδαμε, δεν συγκλίνει συμπεραίνουμε ότι δεν είναι φραγμένη (αν ήταν θα
έπρεπε να συγκλίνει - σύμφωνα με γνωστό θεώρημα) και άρα
συγκλίνει στο ![]() ,
(γιατί;).
,
(γιατί;).