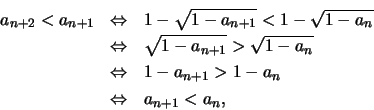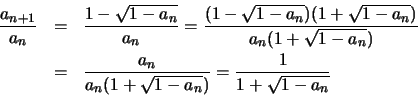Next: 'Ασκηση 15
Up: 'Ασκηση 14
Previous: Υπόδειξη
Λύση
Με επαγωγή δείχνουμε ότι
Πράγματι για 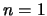 ισχύει από την υπόθεση. Έστω ότι ισχύει για
ισχύει από την υπόθεση. Έστω ότι ισχύει για 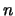 ,
θα δείξουμε ότι ισχύει για
,
θα δείξουμε ότι ισχύει για 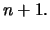 'Εχουμε
'Εχουμε
που ισχύει από την υπόθεση της επαγωγής. Επίσης λόγω της ανισότητας
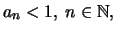 έχουμε ότι η ακολουθία είναι καλώς ορισμένη, δηλαδή η ποσότητα
έχουμε ότι η ακολουθία είναι καλώς ορισμένη, δηλαδή η ποσότητα
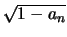 που υπάρχει στον αναδρομικό τύπο ορίζεται για καθε
που υπάρχει στον αναδρομικό τύπο ορίζεται για καθε
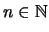 .
.
Στη συνέχεια θα δείξουμε επαγωγικά ότι η ακολουθία είναι φθίνουσα. 'Εχουμε
που ισχύει λόγω της υπόθεσης.
'Εστω 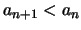 ,
θα δείξουμε ότι
,
θα δείξουμε ότι
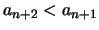 .
Πράγματι
.
Πράγματι
που ισχύει λόγω της υπόθεσης της επαγωγής. 'Αρα η ακολουθία είναι φθίνουσα και
φραγμένη, οπότε συγκλίνει έστω στο 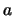 .
Από τον αναδρομικό τύπο έχουμε
.
Από τον αναδρομικό τύπο έχουμε
Η τιμή 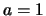 απορρίπτεται αφού η ακολουθία είναι φθίνουσα και
απορρίπτεται αφού η ακολουθία είναι φθίνουσα και 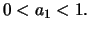 Η δεύτερη γίνεται
δεκτή και άρα
Η δεύτερη γίνεται
δεκτή και άρα
Στη συνέχεια θα υπολογίσουμε το
όριο
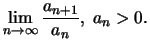 'Εχουμε
'Εχουμε
και άρα, επειδή
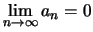 έχουμε
έχουμε
'Ασκηση 14
Υπόδειξη
Antonis Tsolomitis
1999-11-11
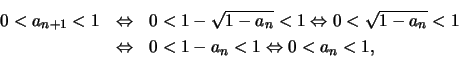
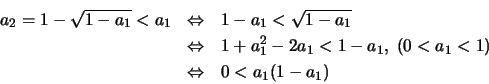
![]() ,
θα δείξουμε ότι
,
θα δείξουμε ότι
![]() .
Πράγματι
.
Πράγματι