


Next: 'Ασκηση 17
Up: 'Ασκηση 16
Previous: Υπόδειξη
Λύση
Θεωρούμε την ακολουθία
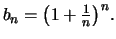 Η ακολουθία
Η ακολουθία
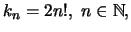 είναι μια γνήσια αύξουσα ακολουθία
φυσικών αριθμών και ισχύει
είναι μια γνήσια αύξουσα ακολουθία
φυσικών αριθμών και ισχύει
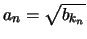 .
Επειδή
.
Επειδή
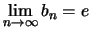 και η
και η 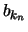 είναι υπακολουθία αυτής
έχουμε ότι
είναι υπακολουθία αυτής
έχουμε ότι
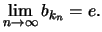 'Αρα σύμφωνα με γνωστή πρόταση
'Αρα σύμφωνα με γνωστή πρόταση
'Ασκηση 16
Υπόδειξη
Antonis Tsolomitis
1999-11-11