Λύση

Δεν μπορούμε να υπολογίσουμε το όριο με βάση τις γνωστές ιδιότητες γιατί εμφανίζεται απροσδιοριστία. Προσπαθούμε να την άρουμε με κατάλληλες πράξεις. 'Εχουμε

$$\begin{eqnarray*} \sqrt {(x+1)(x+2)} - x &= &\frac{( \sqrt {(x+1)(x+2)} - x) (\s... ...{2}{x}}{ \sqrt {(1+\frac{1}{x})(1+\frac{2}{x})} + 1},\; x\not=0. \end{eqnarray*}$$

’ρα

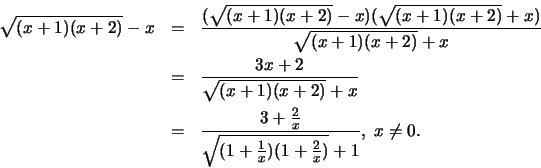
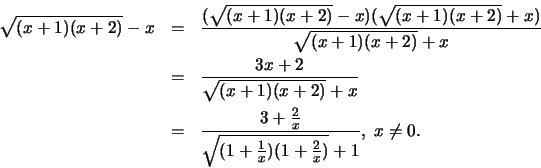
$$\lim\limits_{x \to \infty} [\sqrt {(x+1)(x+2)} - x] = \lim\li... ...x}}{ \sqrt {(1+\frac{1}{x})(1+\frac{2}{x})} + 1} = \frac{3}{2}.$$

'Ασκηση 2 Υπόδειξη