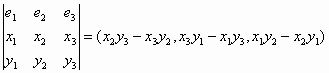
ΚΕΦΑΛΑΙΟ 3
ΤΟ ΕΞΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ
Ορισμός:
Έστω Χ=(x1, x2, x3 ) και Υ=(y1, y2, y3) δύο διανύσματα στον R3. Το εξωτερικό τους γινόμενο Χ 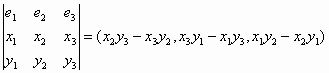
Δεν είναι δύσκολο να δούμε ότι το Χ![]() Υ
Υ
Ιδιότητες
του εξωτερικού γινομένου1. Χ![]() Υ
Υ
2. Χ![]()
3. (αΧ)![]() Υ
= α(Χ
Υ
= α(Χ![]() Υ)
= Χ
Υ)
= Χ![]() (αΥ)
για κάθε πραγματικό α
(αΥ)
για κάθε πραγματικό α
4. (Χ![]() Υ)
Υ)![]() Ζ
= (Χ· Ζ)Υ- (Υ·
Ζ)Χ
Ζ
= (Χ· Ζ)Υ- (Υ·
Ζ)Χ
5. (Χ![]() Υ)^
Χ και (Χ
Υ)^
Χ και (Χ![]() Υ)^
Υ
Υ)^
Υ
6. ½ ½ Χ![]() Υ½
½ = ½ ½
Χ½ ½
½ ½ Y½
½ ½ sinθ½
( δηλαδή η
ποσότητα ½ ½ Χ
Υ½
½ = ½ ½
Χ½ ½
½ ½ Y½
½ ½ sinθ½
( δηλαδή η
ποσότητα ½ ½ Χ![]() Υ½
½ είναι το εμβαδόν του
παραλληλογράμμου που σχηματίζουν τα Χ, Υ)
Υ½
½ είναι το εμβαδόν του
παραλληλογράμμου που σχηματίζουν τα Χ, Υ)
Ασκήσεις
1. Να υπολογίσετε τα Χ![]() Υ,
Υ
Υ,
Υ![]() Χ
και το εμβαδόν του παραλληλογράμμου που
σχηματίζουν τα Χ, Υ,
όταν Χ=(1, 1, 1) και Υ=(2, -2, 2).
[Λύση]
Χ
και το εμβαδόν του παραλληλογράμμου που
σχηματίζουν τα Χ, Υ,
όταν Χ=(1, 1, 1) και Υ=(2, -2, 2).
[Λύση]
2. Να δειχθεί ότι για κάθε Χ
στον R3 έχουμε Χ3. Είναι τα διανύσματα Χ![]()
4. Να υπολογίσετε το εμβαδόν του τριγώνου με κορυφές
τα σημεία (1, -1, 1), (0, 0, 0) και (-2, 3, 0). [Λύση]5. Έστω Α, Β δοθέντα
(μη μηδενικά) κάθετα διανύσματα. Να επιλυθεί η εξίσωση6. Να αποδειχθεί
ότι ||Α![]() Β||2
= ||Α||2 ||Β||2
– (Α· Β)2.
[Λύση] [Επιστροφή
στην άσκ.2 του κεφ.
10]
Β||2
= ||Α||2 ||Β||2
– (Α· Β)2.
[Λύση] [Επιστροφή
στην άσκ.2 του κεφ.
10]