


Next: Ασκήσεις
Up: Τοπολογία του 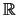 Previous: Τοπολογία του
Previous: Τοπολογία του 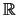
Ορισμός 1
Αν
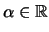
και
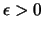
ονομάζουμε
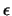 -περιοχή
-περιοχή του
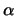
ή
περιοχή κέντρου 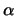 και ακτίνας
και ακτίνας 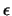
και συμβολίζουμε
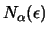
το σύνολο όλων των αριθμών
που έχουν απόσταση από το
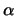
μικρότερη από
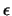
.
Δηλαδή
Είναι φανερό ότι αν
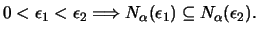
Ορισμός 2
Ένα υποσύνολο

του
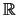
λέγεται
ανοικτό αν για οποιοδήποτε σημείο
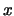
του

υπάρχει κάποια περιοχή
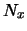
του
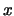
που περιέχεται στο
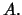
Δηλαδή, για κάθε
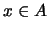
υπάρχει
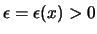
ώστε
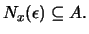
Ορισμός 3
Ένα υποσύνολο

του
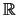
θα το λέμε
κλειστό αν έχει την εξής ιδιότητα: αν
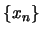
είναι οποιαδήποτε ακολουθία που κάθε όρος της ανήκει στο

(λέμε τότε: η
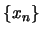
είναι στο

)
και
που συγκλίνει σε κάποιο
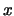
,
τότε το όριό της
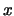
ανήκει και αυτό στο
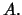
Τα ανοικτά διαστήματα 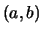 είναι ανοικτά σύνολα ενώ τα κλειστά διαστήματα
είναι ανοικτά σύνολα ενώ τα κλειστά διαστήματα ![$[a, b]$](img20.gif) κλειστά σύνολα. Υπάρχουν και σύνολα
που είναι ανοικτά και κλειστά όπως το
κλειστά σύνολα. Υπάρχουν και σύνολα
που είναι ανοικτά και κλειστά όπως το
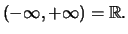
Θεώρημα 4
Ένα υποσύνολο

του
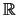
είναι ανοικτό αν και μόνο αν το συμπληρωμά του είναι κλειστό.
Η ένωση ανοικτών συνόλων δίνει ανοικτό σύνολο. Η τομή κλειστών συνόλων δίνει κλειστό σύνολο. Η ένωση πεπερασμένου πλήθους
κλειστών συνόλων δίνει κλειστό σύνολο και η τομή πεπερασμένου πλήθους ανοικτών συνόλων δίνει ανοικτό σύνολο.
Ορισμός 5
Έστω
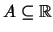
και
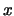
σημείο του

.
Το
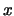
λέγεται
εσωτερικό σημείο του

αν υπάρχει περιοχή
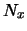
που περιέχεται στο

.
Το σύνολο που έχει σαν στοιχεία του όλα τα εσωτερικά σημεία του

(και μόνο αυτά)
λέγεται
εσωτερικό του

και γράφεται
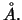
Προφανώς
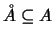
και

ανοικτό αν και μόνο αν
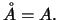
Το
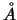
είναι το μεγαλύτερο ανοικτό σύνολο που περιέχεται στο

.
Ορισμός 6
Έστω
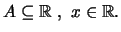
Το
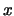
λέγεται
σημείο επαφής του

αν
υπάρχει ακολουθία
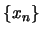
στο

ώστε
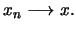
Το σύνολο που έχει σαν στοιχεία όλα τα σημεία επαφής του

(και μόνο αυτά) λέγεται
κλειστή θήκη του

και γράφεται
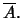
Φανερά
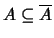 και
και  κλειστό αν και μόνο αν
κλειστό αν και μόνο αν
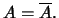 Το
Το 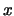 είναι σημείο επαφής του
είναι σημείο επαφής του  αν και μόνο αν κάθε περιοχή
αν και μόνο αν κάθε περιοχή 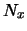 του
του 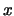 περιέχει τουλάχιστον ένα σημείο του
περιέχει τουλάχιστον ένα σημείο του 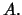 To
To 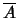 είναι το μικρότερο κλειστό σύνολο που περιέχει το
είναι το μικρότερο κλειστό σύνολο που περιέχει το 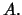
Ορισμός 7
Αν
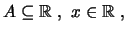
το
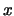
λέγεται
συνοριακό σημείο του

αν κάθε περιοχή
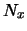
περιέχει και σημείο του

και σημείο του
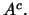
Το σύνολο που περιέχει όλα τα συνοριακά σημεία του

(και μόνο αυτά) λέγεται
σύνορο του

και γράφεται
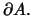
Θεώρημα 8
Έστω
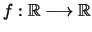
.
Τα ακόλουθα είναι ισοδύναμα
(α) Η
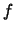
είναι συνεχής στο
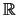
(β) Για κάθε ανοικτό
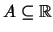
το
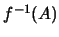
είναι ανοικτό υποσύνολο του
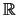
(γ) Για κάθε κλειστό
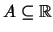
το
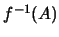
είναι κλειστό υποσύνολο του
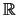
root
1999-07-29
![]()