


Next: Άσκηση 8
Up: Άσκηση 7
Previous: Υπόδειξη
Λύση
(α) Το 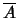 είναι κλειστό, άρα ταυτίζεται με την κλειστή του θήκη:
είναι κλειστό, άρα ταυτίζεται με την κλειστή του θήκη:
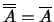 .
Έχουμε
.
Έχουμε
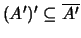 και από το
και από το 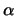 το
το 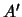 είναι κλειστό. Άρα,
είναι κλειστό. Άρα,
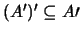 .
Δεν ισχύει πάντα ισότητα: Αν
.
Δεν ισχύει πάντα ισότητα: Αν
 .
.
(β) Για κάθε
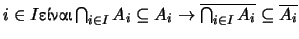 .
Άρα,
.
Άρα,
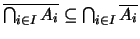 .
Άν
.
Άν
![$A=(0, 1), B=(1, 2), \ \hbox{τότε}\ \overline{A} =[0, 1]\ ,\ \overline{B}=[1, 2] \ \hbox{άρα}
\ \overline{A} \cap \overline{B} = \{ 1 \}$](img118.gif) ,
ενώ
,
ενώ
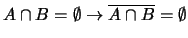 .
.
(γ) Το 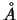 είναι ανοικτό, άρα ταυτίζεται με το εσωτερικό του.
είναι ανοικτό, άρα ταυτίζεται με το εσωτερικό του.
Άσκηση 7
Υπόδειξη
root
1999-07-29
![]() .
Άρα,
.
Άρα,
![]() .
Άν
.
Άν
![]() ,
ενώ
,
ενώ
![]() .
.
![]() είναι ανοικτό, άρα ταυτίζεται με το εσωτερικό του.
είναι ανοικτό, άρα ταυτίζεται με το εσωτερικό του.