


Next: Άσκηση 32
Up: Άσκηση 31
Previous: Υπόδειξη
Έστω ότι τέτοιος πίνακας 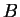 υπάρχει. Τότε
υπάρχει. Τότε 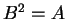 και
και
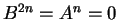 άρα ο
άρα ο 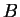 είναι μηδενοδύναμος. Από προηγούμενα
αποτελέσματα έχουμε ότι το χαρακτηριστικό πολυώνυμο του
είναι μηδενοδύναμος. Από προηγούμενα
αποτελέσματα έχουμε ότι το χαρακτηριστικό πολυώνυμο του 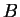 είναι
το
είναι
το 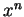 και από το Θεώρημα Cayley - Hamilton έχουμε ότι
και από το Θεώρημα Cayley - Hamilton έχουμε ότι 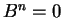 .
Αν τώρα ο
.
Αν τώρα ο 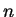 είναι άρτιος, δηλαδή
είναι άρτιος, δηλαδή 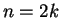 τότε
τότε 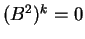 το
οποίο συνεπάγεται ότι
το
οποίο συνεπάγεται ότι 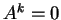 άτοπο γιατί
άτοπο γιατί 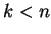 και από υπόθεση
και από υπόθεση
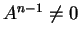 .
Αν ο
.
Αν ο 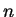 είναι περιττός,
είναι περιττός, 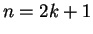 τότε
τότε
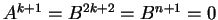 και
και 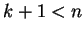 ,
το οποίο είναι άτοπο από
την υπόθεση. Άρα δεν υπάρχει πίνακας
,
το οποίο είναι άτοπο από
την υπόθεση. Άρα δεν υπάρχει πίνακας 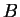 ώστε
ώστε 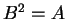 .
.
Vassilis Metaftsis
1999-09-15