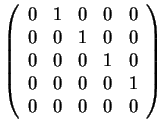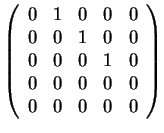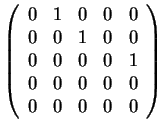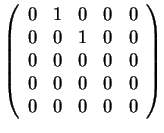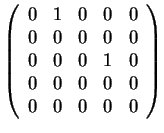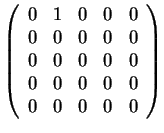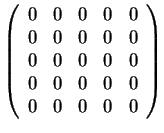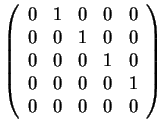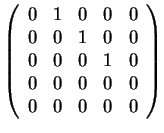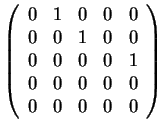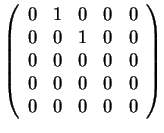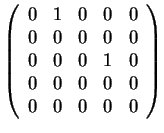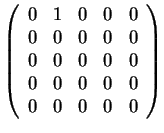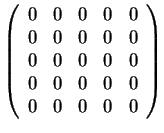Next: Δυϊκοί Χώροι
Up: Άσκηση 32
Previous: Υπόδειξη
Το χαρακτηριστικό πολυώνυμο ενός μηδενοδύναμου 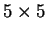 πίνακα
είναι το
πίνακα
είναι το 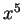 .
Άρα οι πιθανοί στοιχειώδεις διαιρέτες και οι αντίστοιχοι
πίνακες είναι οι εξής
.
Άρα οι πιθανοί στοιχειώδεις διαιρέτες και οι αντίστοιχοι
πίνακες είναι οι εξής
- .
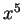 ,
,
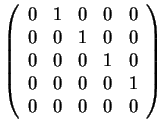
- .
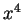 ,
,
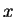 ,
,
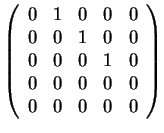
- .
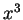 ,
,
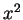 ,
,
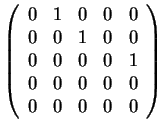
- .
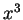 ,
,
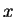 ,
,
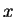 ,
,
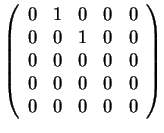
- .
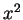 ,
,
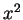 ,
,
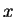 ,
,
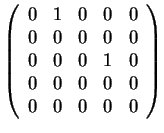
- .
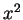 ,
,
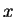 ,
,
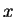 ,
,
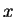 ,
,
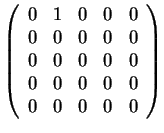
- .
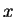 ,
,
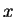 ,
,
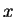 ,
,
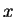 ,
,
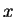 ,
,
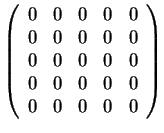
Vassilis Metaftsis
1999-09-15