


Next: Άσκηση 33
Up: Δυϊκοί Χώροι
Previous: Δυϊκοί Χώροι
Ορισμός 11
Έστω

διανυσματικός χώρος πάνω στο σώμα
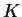
.
Το σύνολο όλων των
γραμμικών απεικονίσεων από το

στο
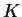
,
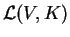
συμβολίζεται
με
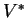
και καλείται δυϊκός χώρος του

.
Τα στοιχεία του
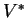
λέγονται
γραμμικές μορφές επάνω στο

.
Πρόταση 5
Aν
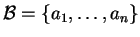
είναι μια διατεταγμένη βάση του διανυσματικού
χώρου

τότε υπάρχει μια μονοσήμαντα ορισμένη διατεταγμένη βάση του
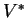
έστω
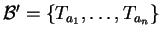
τέτοια ώστε
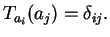
Πόρισμα 5
Oι διανυσματικοί χώροι

και
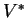
έχουν την ίδια διάσταση και για κάθε

με
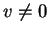
υπάρχει

τέτοια ώστε
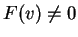
.
Θεώρημα 18
Έστω
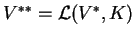
και ορίζω
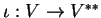
με
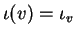
να είναι η γραμμική απεικόνιση
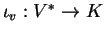
η οποία απεικονίζει
το

στο
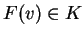
.
Η απεικόνιση
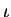
είναι ισομορφισμός.
Ορισμός 12
Έστω

διανυσματικός χώρος και
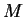
υπόχωρος του

.
Το σύνολο
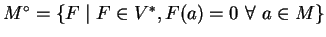
λέγεται
μηδενιστής του
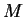
.
Πρόταση 6
O μηδενιστής
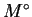
ενός διανυσματικού υπόχωρου
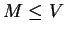
είναι
διανυσματικός υπόχωρος.
Θεώρημα 20
Αν
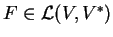
και
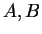
οι πίνακες τις
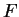
ως προς δύο
διαφορετικές βάσεις του

τότε υπάρχει αντιστρέψιμος πίνακας
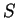
τέτοιος
ώστε
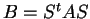
.
Σε αυτή την περίπτωση οι πίνακες

και
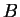
λέγονται
ισότιμοι.
Vassilis Metaftsis
1999-09-15