Ορισμός 13
Έστω
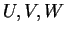
διανυσματικοί χώροι στο σώμα
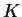
και
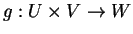
μια απεικόνιση. Η
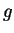
λέγεται διγραμμική αν για κάθε
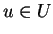
η απεικόνιση
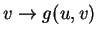
είναι γραμμική και για κάθε

η
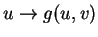
είναι
γραμμική. Δηλαδή η
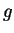
ικανοποιεί τις συνθήκες
για κάθε
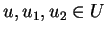
,
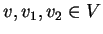
και
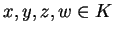
.
To σύνολο όλων των διγραμμικών απεικονίσεων συμβολίζεται με
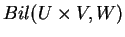 .
.
Θεώρημα 21
Αν
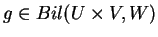
τότε υπάρχει μοναδικός πίνακας

τέτοιος
ώστε
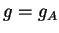
,
δηλαδή
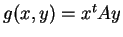
.
H απεικόνιση η οποία στέλνει κάθε πίνακα  διάστασης
διάστασης 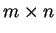 στην
αντίστοιχη διγραμμική μορφή
στην
αντίστοιχη διγραμμική μορφή 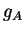 είναι ισομορφισμός, δηλαδή
είναι ισομορφισμός, δηλαδή
Ορισμός 14
Έστω

διανυσματικός χώρος πάνω στο σώμα
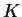
με εσωτερικό γινόμενο. Τότε
η απεικόνιση
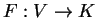
με
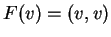
λέγεται τετραγωνική μορφή.
![]() .
.![]() .
.![]() διάστασης
διάστασης ![]() στην
αντίστοιχη διγραμμική μορφή
στην
αντίστοιχη διγραμμική μορφή ![]() είναι ισομορφισμός, δηλαδή
είναι ισομορφισμός, δηλαδή