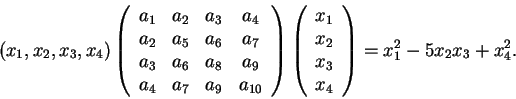Next: Eρμιτιανές και Συμμετρικές απεικονίσεις
Up: Άσκηση 40
Previous: Υπόδειξη
Έστω
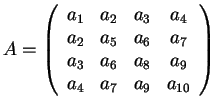 ο πίνακας της τετραγωνικής μορφής. Τότε
ο πίνακας της τετραγωνικής μορφής. Τότε
Λύνουμε το σύστημα και παίρνουμε 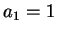 ,
,
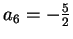 ,
,
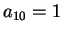 ,
,
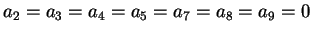 .
Άρα η διγραμμική μορφή που αντιστοιχεί στον
.
Άρα η διγραμμική μορφή που αντιστοιχεί στον  είναι η
είναι η
Vassilis Metaftsis
1999-09-15
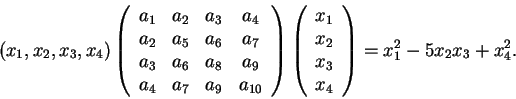
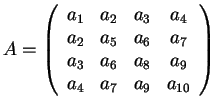 ο πίνακας της τετραγωνικής μορφής. Τότε
ο πίνακας της τετραγωνικής μορφής. Τότε