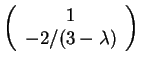 .
Αντικαθιστώντας
.
Αντικαθιστώντας 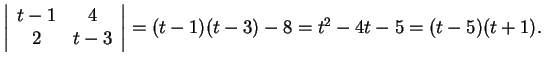 Άρα οι
ιδιοτιμές του πίνακα είναι
Άρα οι
ιδιοτιμές του πίνακα είναι 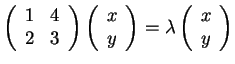 το οποίο δίνει τις εξισώσεις
το οποίο δίνει τις εξισώσεις
Θέτουμε ![]() και βρίσκουμε
και βρίσκουμε
![]() .
Άρα τα
ιδιοδιανύσματα του πίνακα έχουν την μορφή
.
Άρα τα
ιδιοδιανύσματα του πίνακα έχουν την μορφή
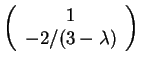 .
Αντικαθιστώντας
.
Αντικαθιστώντας ![]() και
και ![]() παίρνω
παίρνω ![]() και
και
![]() .
Άρα για την ιδιοτιμή 5 ο ιδιόχωρος (που είναι
μονοδιάστατος) έχει βάση το
.
Άρα για την ιδιοτιμή 5 ο ιδιόχωρος (που είναι
μονοδιάστατος) έχει βάση το ![]() και για την ιδιοτιμή -1 ο
μονοδιάστατος υπόχωρος που παράγεται έχει βάση το
και για την ιδιοτιμή -1 ο
μονοδιάστατος υπόχωρος που παράγεται έχει βάση το ![]() .
Παρατηρήστε ότι αν αντικαθιστούσαμε το
.
Παρατηρήστε ότι αν αντικαθιστούσαμε το ![]() με οποιονδήποτε άλλον
αριθμό (εκτός του 1) θα παίρναμε αντί των
με οποιονδήποτε άλλον
αριθμό (εκτός του 1) θα παίρναμε αντί των ![]() κάποια
πολλαπλάσιά τους. Επομένως δεν θα άλλαζαν ούτε οι ιδιόχωροι ούτε
βέβαια η διάστασή τους.
κάποια
πολλαπλάσιά τους. Επομένως δεν θα άλλαζαν ούτε οι ιδιόχωροι ούτε
βέβαια η διάστασή τους.