Στοιχεία Θεωρίας

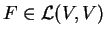
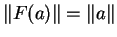
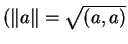
Ορισμός 15   Σε έναν διανυσματικό χώρο $V$ με θετικά ορισμένο εσωτερικό γινόμενο μια γραμμική απεικόνιση $F\in {\cal L}(V,V)$ λέγεται ισομετρία αν $\Vert F(a)\Vert=\Vert a\Vert$ $(\Vert a\Vert=\sqrt{(a,a)}$ για κάθε $a\in V$.

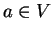
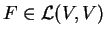
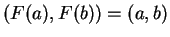
Πρόταση 9   Mια γραμμική απεικόνιση $F\in {\cal L}(V,V)$ είναι ισομετρία αν και μόνο αν $(F(a),F(b))=(a,b)$ για κάθε $a,b\in V$.

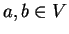
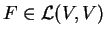
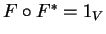
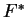
Πρόταση 10   Mια γραμμική απεικόνιση $F\in {\cal L}(V,V)$ είναι ισομετρία αν και μόνο αν $F\circ F^*=1_V$ όπου $F^*$ είναι η δυϊκή απεικόνιση της $F$.

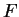
Πόρισμα 7   Αν $A$ ο πίνακας μιας ισομετρίας ως προς μια ορθοκανονική βάση τότε $AA^*=I.$

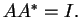
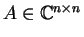
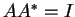
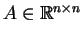
Ορισμός 16   Ενας πίνακας $A\in \mathbb C^{n\times n}$ λέγεται μοναδιαίος αν $AA^*=I$. Ενας πίνακας $A\in \mathbb R^{n\times n}$ λέγεται ορθογώνιος αν $AA^t=I$.

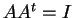
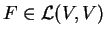
Πρόταση 11   Μια γραμμική απεικόνιση $F\in {\cal L}(V,V)$ είναι ισομετρία αν και μόνο αν απεικονίζει κάθε ορθοκανονική βάση σε ορθοκανονική βάση.

Πόρισμα 8   Ο πίνακας αλλαγής από μια ορθοκανονική σε μια άλλη ορθοκανονική βάση είναι μοναδιαίος (ή ορθογώνιος).

Θεώρημα 24   Ένας πίνακας είναι μοναδιαίος (ορθογώνιος) αν και μόνο αν οι γραμμές του αποτελούν ορθοκανονική βάση.