


Next: Άσκηση 6
Up: Άσκηση 5
Previous: Υπόδειξη
Το χαρακτηριστικό πολυώνυμο του πίνακα είναι
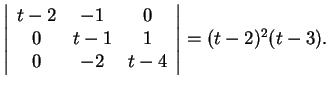 Άρα οι ιδιοτιμές του πίνακα
είναι το 2 (διπλή) και το 3. Αν τώρα
Άρα οι ιδιοτιμές του πίνακα
είναι το 2 (διπλή) και το 3. Αν τώρα 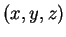 είναι ένα
ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
είναι ένα
ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή 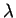 τότε εργαζόμενοι
όπως προηγούμενα παίρνουμε το σύστημα
τότε εργαζόμενοι
όπως προηγούμενα παίρνουμε το σύστημα
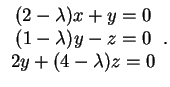 Για
Για 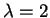 παίρνουμε το διάνυσμα
παίρνουμε το διάνυσμα 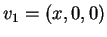 και άρα
o ιδιόχωρος που παράγεται είναι μονοδιάστατος και μιά βάση του είναι
το διάνυσμα
και άρα
o ιδιόχωρος που παράγεται είναι μονοδιάστατος και μιά βάση του είναι
το διάνυσμα 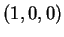 .
.
Για 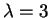 το διάνυσμα που παίρνω είναι το
το διάνυσμα που παίρνω είναι το 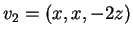 .
Άρα ο
ιδιόχωρος που παράγεται είναι μονοδιάστατος και μια βάση του είναι
το διάνυσμα
.
Άρα ο
ιδιόχωρος που παράγεται είναι μονοδιάστατος και μια βάση του είναι
το διάνυσμα 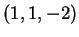 .
.
Vassilis Metaftsis
1999-09-15
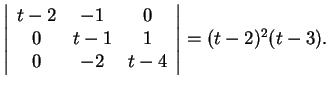 Άρα οι ιδιοτιμές του πίνακα
είναι το 2 (διπλή) και το 3. Αν τώρα
Άρα οι ιδιοτιμές του πίνακα
είναι το 2 (διπλή) και το 3. Αν τώρα 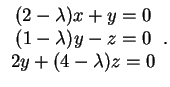 Για
Για ![]() το διάνυσμα που παίρνω είναι το
το διάνυσμα που παίρνω είναι το ![]() .
Άρα ο
ιδιόχωρος που παράγεται είναι μονοδιάστατος και μια βάση του είναι
το διάνυσμα
.
Άρα ο
ιδιόχωρος που παράγεται είναι μονοδιάστατος και μια βάση του είναι
το διάνυσμα ![]() .
.