


Next: Άσκηση 13
Up: Διαγωνοποιήσιμοι Πίνακες
Previous: Διαγωνοποιήσιμοι Πίνακες
Ορισμός 5
Ένας πίνακας λέγεται διαγώνιος αν όλα τα στοιχεία του εκτός της κυρίας
διαγωνίου είναι μηδενικά. Ένας πίνακας λέγεται διαγωνοποιήσιμος αν
είναι όμοιος με έναν διαγώνιο πίνακα. Μια γραμμική απεικόνιση
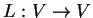
λέγεται διαγωνοποιήσιμη αν ο

έχει μια βάση τέτοια ώστε ο πίνακας
της
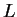
ως προς την βάση αυτή να είναι διαγώνιος.
Πρόταση 2
Mια γραμμική απεικόνιση
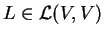
είναι διαγωνοποιήσιμη αν ο

έχει μια βάση που αποτελείται από ιδιοδιανύσματα της
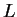
.
Πρόταση 3
Αν
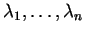
είναι διαφορετικές ανα δύο ιδιοτιμές μιας
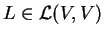
και
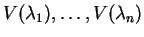
είναι οι ιδιόχωροι
που αντιστοιχούν στις ιδιοτιμές τότε το άθροισμα
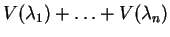
είναι ευθύ, δηλαδή
Θεώρημα 9
Aν
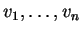
είναι ιδιοδιανύσματα γραμμικής απεικόνισης που
αντιστοιχούν σε διακεκριμένες ιδιοτιμές τότε τα
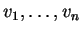
είναι
γραμμικώς ανεξάρτητα.
Θεώρημα 10
Έστω
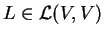
.
Αν
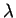
μια ιδιοτιμή της
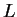
τότε η διάσταση του
ιδιόχωρου που αντιστοιχεί στην ιδιοτιμή
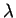
είναι μικρότερη ή ίση με την
πολλαπλότητα του
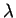
σαν ρίζα του χαρακτηριστικού πολυωνύμου.
Θεώρημα 11
Mια γραμμική απεικόνιση
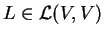
είναι διαγωνοποιήσιμη αν και
μόνο αν
όπου
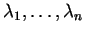
είναι οι διακεκριμένες ιδιοτιμές της
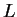
.
Πόρισμα 1
Αν η γραμμική απεικόνιση
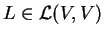
είναι διαγωνοποιήσιμη και
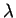
είναι μια ιδιοτιμή της τότε η διάσταση του ιδιόχωρου που αντιστοιχεί
στην ιδιοτιμή αυτή είναι ίση με την πολλαπλότητα του
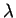
σαν ρίζα
του χαρακτηριστικού πολυωνύμου.
Θεώρημα 12
Mια γραμμική απεικόνιση
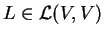
είναι διαγωνοποιήσιμη αν και
μόνο αν το ελάχιστο πολυώνυμο της
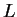
είναι γινόμενο διακεκριμένων
πρωτοβάθμιων παραγόντων,
όπου
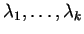
διακεκριμένες
ιδιοτιμές της
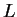
.
Vassilis Metaftsis
1999-09-15