


Next: Άσκηση 15
Up: Άσκηση 14
Previous: Υπόδειξη
Το χαρακτηριστικό πολυώνυμο του πίνακα είναι το
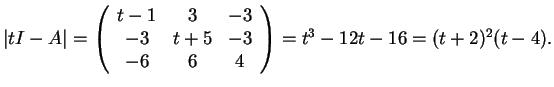 Άρα οι ιδιοτιμές του
Άρα οι ιδιοτιμές του  είναι
είναι 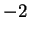 και
και
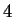 .
Για την ιδιοτιμή
.
Για την ιδιοτιμή 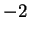 έχω
έχω
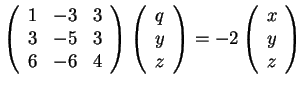 το οποίο δίνει το σύστημα
το οποίο δίνει το σύστημα
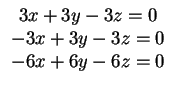 το οποίο έχει δύο ανεξάρτητες μεταβλήτές και άρα τα διανύσματα
το οποίο έχει δύο ανεξάρτητες μεταβλήτές και άρα τα διανύσματα
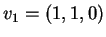 και
και 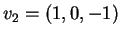 είναι γραμμικώς ανεξάρτητα και
αντιστοιχούν στην ιδιοτιμή
είναι γραμμικώς ανεξάρτητα και
αντιστοιχούν στην ιδιοτιμή 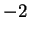 .
Όμοια για την ιδιοτιμή 4 παίρνω το σύστημα
.
Όμοια για την ιδιοτιμή 4 παίρνω το σύστημα
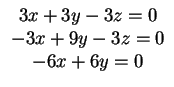 το οποίο έχει μια ανεξάρτητη μεταβλήτη και άρα το
το οποίο έχει μια ανεξάρτητη μεταβλήτη και άρα το 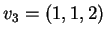 είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή 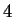 .
Άρα το
σύνολο
.
Άρα το
σύνολο
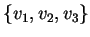 είναι ένα σύνολο από ιδιοδιανύσματα τα
οποία είναι γραμμικώς ανεξάρτητα και άρα απότελούν βάση του
είναι ένα σύνολο από ιδιοδιανύσματα τα
οποία είναι γραμμικώς ανεξάρτητα και άρα απότελούν βάση του
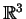 .
Άρα ο
.
Άρα ο  είναι διαγωνοποιήσιμος και ο ζητούμενος πίνακας
είναι διαγωνοποιήσιμος και ο ζητούμενος πίνακας
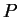 είναι ο πίνακας με στήλες τα
είναι ο πίνακας με στήλες τα 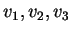 ,
δηλαδή
,
δηλαδή
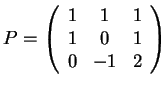 .
Εύκολα βλέπει κανείς ότι
.
Εύκολα βλέπει κανείς ότι
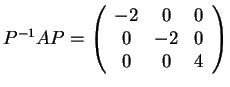 .
.
Vassilis Metaftsis
1999-09-15
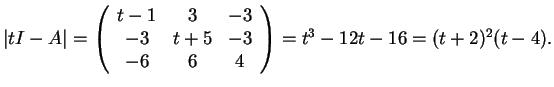 Άρα οι ιδιοτιμές του
Άρα οι ιδιοτιμές του 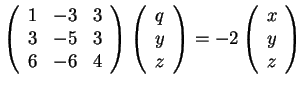 το οποίο δίνει το σύστημα
το οποίο δίνει το σύστημα
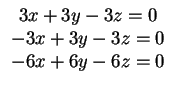 το οποίο έχει δύο ανεξάρτητες μεταβλήτές και άρα τα διανύσματα
το οποίο έχει δύο ανεξάρτητες μεταβλήτές και άρα τα διανύσματα
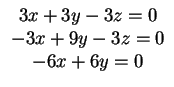 το οποίο έχει μια ανεξάρτητη μεταβλήτη και άρα το
το οποίο έχει μια ανεξάρτητη μεταβλήτη και άρα το 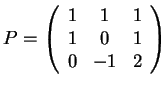 .
Εύκολα βλέπει κανείς ότι
.
Εύκολα βλέπει κανείς ότι
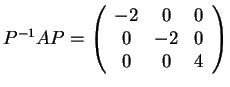 .
.